سكين الحذاء (هندسة)

سكين الحذّاء.

في الهندسة الرياضية، سكين الحذَّاء (بالإنجليزية: Arbelos)‏ هي منطقة مستوية محصورة بثلاث أنصاف دوائر لها ثلاث قمم, بحيث أن كل نصف دائرة تشترك بكل زاوية من زواياها مع أحد أنصاف الدوائر الأخرى, وكل أنصاف الدوائر تكون على الجهة نفسها على خط مستقيم (القاعدة).

يعتقد أن أرخميدس هو أول من درس هذا الشكل ووضع خصائصه الرياضية. «Arbelos» تعني حرفياً «سكين الحذَّاء» باللغة الإغريقية. وتمثل نصلة السكين التي استخدمت من قبل صانعي الأحذية في القدم.

خصائص

بعض النقاط المميزة لشكل سكين الحذاء

إثنتان من أنصاف الدوائر يجب أن تكونا مقعرتين, ولهما أيُّ قطران أ و ب. الدائرة الثالثة تكون محدبة, ولها القطر أ + ب.

المساحة

مساحة شكل سكين الحذاء تساوي مساحة دائرة لها القطر HA.

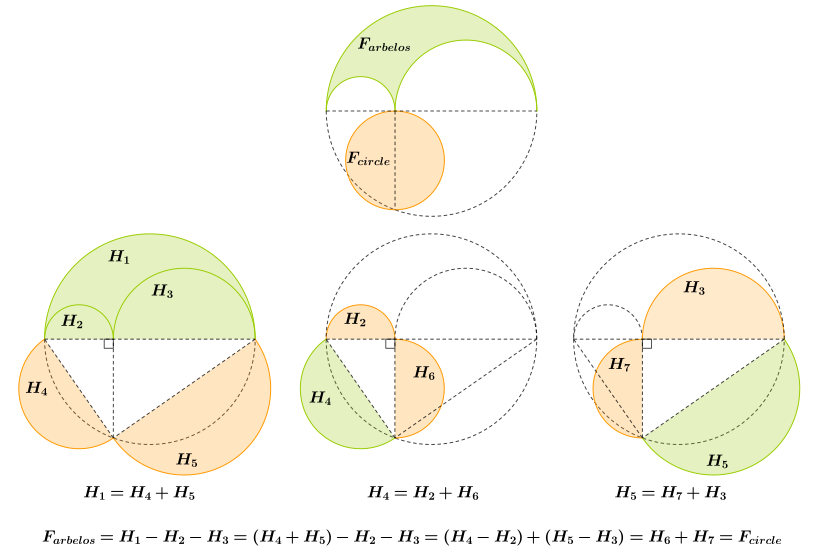
برهان: للبرهنة على ذلك, إعكس الشكل على الخط المار عبر النقطتين B و C, لاحظ أن ضعف مساحة سكين الحذاء هو ما يتبقى عندما تُطرَح مساحة الدائرتين الأصغر (اللتان لهما القطران BA وAC) من مساحة الدائرة الأكبر (التي لها القطر BC). حيث أن مساحة الدائرة تناسبية مع مربع القطر (الأصول لإقليدس, الكتاب الثاني عشر (12), البرهان الثاني (2); لا نحتاج أن نعرف أن ثابت التناسب هو π/4), المعادلة تؤول إلى إثبات أن $2|AH|^{2}=|BC|^{2}-|AC|^{2}-|BA|^{2}$. الطول |BC| يساوي مجموع الطولين |BA| و |AC|, فتُبسَّط المعادلة جبرياً إلى أن $|AH|^{2}=|BA||AC|$. فيكون الإدِّعاء هو أن طول القطعة AH يساوي المتوسط الهندسي لطول القطعتين BA و AC. الآن (في الرسم التوضيحي) المثلث BHC, نتيجة لاحتوائه في نصف الدائرة, يكون له زاوية قائمة عند النقطة H (الأصول لإقليدس, الكتاب الثالث (3), البرهان الواحد والثلاثون (31)), وبالتالي |HA| تكون بالفعل متوسط تناسب بين |BA| و |AC| (الأصول لإقليدس, الكتاب السادس (6), البرهان الثامن (8)). هذا البرهان يقارب الحجة الإغريقية القديمة; إستَشهَد هارولد بي بواس بورقة لروجر بي نلسن الذي طبق الفكرة كبرهان لا كلامي كالآتي.