اتحاد (نظرية المجموعات)
المظهر
اتحاد
| صنف فرعي من | |
|---|---|
| تعريف الصيغة | |
| الرموز في الصيغة | |
| ممثلة بـ | |
| سلسلة محارف لاتكس (LaTeX) | |
| النقيض |

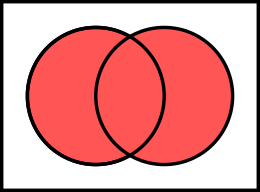
في نظرية المجموعات، يشير مصطلح الاجتماع أو الاتحاد إلى العملية على المجموعات التي تستخدم في دمج مجموعتين للحصول على مجموعة جديدة تحوي عناصر كلا المجموعتين.[1][2]
كمثال بسيط على هذه العملية، إن اجتماع مجموعتين منفصلتين لا تشتركان بأي عنصر هو المجموعتان ذاتهما.
اتحاد مجموعتين
[عدل]اتحاد مجموعتين A و B هو مجموعة. و تتكون من العناصر التي تنتمي إلى المجموعة A أو المجموعة B . و نرمز له ب A ∪ B.
رياضيا نكتب :
مثال : اتحاد المجموعة {1,2,3} و المجموعة {2,3,4} هو المجموعة {1,2,3,4}.
الخصائص الجبرية
[عدل]- الاتحاد عملية تجميعية. لتكن A, B, C مجموعات. لدينا:
- الاتحاد عملية تبديلية. لتكن A, B مجموعتين. لدينا :
A ∪ B = B ∪ A - التقاطع توزيعي بالنسبة للاتحاد. لتكن A, B, C مجموعات. لدينا :
(A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C
انظر أيضاً
[عدل]مراجع
[عدل]- ^ "معلومات عن اتحاد (نظرية المجموعات) على موقع britannica.com". britannica.com. مؤرشف من الأصل في 2019-12-10.
- ^ "معلومات عن اتحاد (نظرية المجموعات) على موقع mathworld.wolfram.com". mathworld.wolfram.com. مؤرشف من الأصل في 2019-04-02.