بوابة:إحصاء/مقالة مختارة
عدد مقاطع المقالات التي تم إحصاؤها هو : 4.
المقالات المختارة
المقالة رقم 1
 مسألة مونتي هول (بالإنجليزية: Monty Hall problem) هي لغز احتمالات ظهر في البرنامج التلفزيوني الأمريكي للألعاب دعونا نعقد صفقة (بالإنجليزية: Let's Make a Deal). أتى اسم هذه المسألة من اسم المضيف مونتي هول. هذه المسألة تسمى أيضًا مفارقة مونتي هول (بالإنجليزية: Monty Hall paradox). فبما أنها مفارقة حقيقية فإن طريقة حلها غير قابلة للتوقُع. نشر التعبير المشهور لهذه المسألة في مجلة باريد(بالإنجليزية: Parade): «افترض بأنك في برنامج للألعاب، وخُيرت بين ثلاثة أبواب: يوجد سيارة وراء واحد من هذه الأبواب، وستجد الماعز وراء الآخريين. عليك أن تختار أحدها، فتختار الباب ذو الرقم 1. سيفتح المضيف -الذي يعرف ما وراء تلك الأبواب- بابًا آخرًا، فلنفترض أنه أختار الباب ذو الرقم 3 الذي وراءه ماعز. سيقول لك: "هل تريد اختيار الباب ذو الرقم 2؟" أليس من صالحك في أن تغير اختيارك؟»
|
المقالة رقم 2
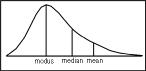 الإحصاء الوصفي هو مجموعة طرائق لوصف الخصائص الرئيسية لمجموعة بيانات كمياً باستخدام الجداول والمخططات البيانية. يشكل الإحصاء الوصفي مع الإحصاء الاستدلالي قسمي علم الإحصاء. وبخلاف الإحصاء الاستدلالي لا تُستخدَم في الإحصاء الوصفي الطرائق الاحتمالية من أجل تعميم النتائج على الجمهرة. الإحصاء الوصفي يهدف إلى وصف مجموعة من البيانات وتنظيمها وتصنيفها وتلخيصها وعرضها بطريقة واضحة في صورة جداول أو أشكال بيانية وحساب المقاييس الإحصائية المختلفة لوصف متغير ما (أو أكثر) في مجتمع ما.
|
المقالة رقم 3
 في الإحصاء ونظرية الاحتمالات، يعتبر الانحراف المعياري (بالإنكليزية: Standard deviation) القيمة الأكثر استخداما من بين مقاييس التشتت الإحصائي لقياس مدى التبعثر الإحصائي، أي أنه يدل على مدى امتداد مجالات القيم ضمن مجموعة البيانات الإحصائية. عادة ما يرمز إلى الانحراف المعياري بالحرف الإغريقي الصغير σ. و التباين وهو معدل مربعات انحرافات العلامات في التوزيع عن الوسط الحسابي. ويكون الانحراف المعياري عندها الجذر التربيعي للتباين بالنسبة لمجموعة البيانات الإحصائية. يتأثر التباين أو الانحراف المعياري بالقيم المتباعدة أو المتطرفة ولكنه لا يتأثر كثيرا بالتغيرات التي تطرأ على العينة, كما أنهما يرتبطان بالوسط الحسابي للتوزيع، بمعنى ان التشتت الذي نعبر عنه بالتباين أو الانحراف المعياري ينسب إلى الوسط الحسابي وليس لاي نقطة أخرى في التوزيع.
|
المقالة رقم 4
 نظرية الاحتمال (بالإنجليزية: Probability theory) هي النظرية التي تدرس احتمال الحوادث العشوائية، بالنسبة للرياضيين، الاحتمالات أعداد محصورة في المجال بين 0 و1 تحدد احتمال حصول أو عدم حصول حدث معين عشوائي أي غير مؤكد. يتم تحديد احتمال الحدث بالقيمة حسب بدهيات الاحتمال. كما ندعو احتمال الحدث علما بحدوث الحدث : الاحتمال الشرطي للحدث مع العلم بحدوث . نمثل هذا الاحتمال الشرطي بالنسبة بين احتمال التقاطع بين الحدثين (أي حدوثهما معا) إلى احتمال حدوث الحدث ، أي . إذا لم تتغير قيمة الاحتمال الشرطي للحدث علما بوقوع عن القيمة الأصلية غير الشرطية للحدث أي أن الاحتمال واحد في حال وقوع أو عدم وقوعه عندئذ نقول أن هذين الحدثين مستقلين. تناقش نظرية الاحتمالات مصطلحين غاية في الأهمية وهما: المتغير العشوائي والتوزيع الاحتمالي للمتغير العشوائي.
|




