بوابة منطقية
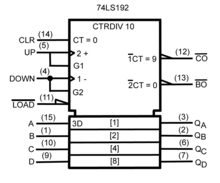
البوابة المنطقية[1] [2] (بالإنجليزية: Logic gate) هي دائرة إلكترونية [3] تحتوي على (مدخل واحد أو عدة مداخل) ومخرج واحد حيث تقوم بعملية منطقية على المدخل وتنتج المخرج المطلوب، تستخدم هذه البوابات في بناء معالجات الأجهزة الإلكترونية والحواسيب.[4][5][6] لأنّ مخرج البوابة الرقمية هو أيضاً قيمة منطقية، فإنّه يمكن استخدام مخرج أحد البوابات المنطقية كمدخل لبوابة أخرى. المنطق المستخدم غالباً هو المنطق البولياني (Boolean logic)، وهو المنطق الذي يعمل في الدوائر الرقمية.
تُصنع الدائرة الإلكترونية للبوابة الرقمية باستخدام دايودات ومقاحل، ويمكن أيضاً بناؤها باستخدام المبدّلات الإلكترونية، سوائل منطقية، إشارات ضوئية، جزيئات، وحتى من أجزاء ميكانيكية.
المستويات المنطقية
[عدل]المستوى في المنطق البوليانى لابد أن يكون أحد مستويين. هذان المستويان لهم أسماء عديدة منها: عالي ومنخفض، مفتوح ومغلق، نعم ولا، حقيقى وكاذب، واحد وصفر.
جدول الحقيقة
[عدل]جدول الحقيقة هو جدول يصف سلوك البوابة المنطقية أو دائرة منطقية(عدة بوابات منطقية) حيث يوضح قيمة المخرج لكل مدخل منطقي محتمل، ويمكن أن يستخدم في تبسيط عدد البوابات المنطقية عند تصميم دائرة منطقية.ولكن بصفة عامة لا يستخدم جدول الحقيقة في التبسيط وإنما تستخدم خريطة كارنو فايتش (karanaugh map).
أنواع التقنيات
[عدل]أهم الأنواع هي منطق المقاومات- المقاحل (الترانزستورات) RTL ومنطق الدايودات -المقاحل DTL ومنطق المقاحل TTL ومنطق الموسفت (ترانزستور معدن -أكسيد -شبه موصل) المتناظر CMOS
| مدخل | A | 0 | 0 | 1 | 1 |
| B | 0 | 1 | 0 | 1 | |
| مخرج | 0 | 0 | 0 | 0 | 0 |
| A> B * | 0 | 0 | 1 | 0 | |
| A | 0 | 0 | 1 | 1 | |
| A <B * | 0 | 1 | 0 | 0 | |
| B | 0 | 1 | 0 | 1 | |
| A ≥ B * | 1 | 0 | 1 | 1 | |
| A ≤ B * | 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 1 | 1 |
البوابات المنطقية هي جزء رئيسي من الكثير من الدوائر الرقمية، لذلك، كل نوع منها مُنتج كدارة متكاملة (IC)، انظر لسلسلة 4000 من عائلة CMOS. أو السلسلة 700.
الرموز
[عدل]يوجد مجموعتان من الرموز القياسية الأولى تعتمد على شكل الرمز وهي الأقدم وما زالت الأكثر انتشارا لسهولتها والأخرى تعتمد على حروف لاتينية داخل مربعات
| نوع | شكل مميز | شكل مستطيلي | الجبر البولياني بين A و B | جدول الحقيقة | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
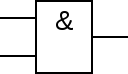
| و AND |
|
| |||||||||||||||||||||
| أو OR |

|
| |||||||||||||||||||||
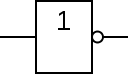
| ليس NOT |
|
| |||||||||||||||||||||
| في الإلكترونيات، غالباً ما تسمى بوابة NOT بالعاكس (Inverter). الدائرة المرسومة أمام رسمة البوابة تدعى الفقاعة (Bubble). وترسم الفقاعة أحياناً أمام أي دائرة منطقية لبيان أنّها معكوسة (active-low). | |||||||||||||||||||||||
| NAND | 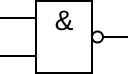
|
| |||||||||||||||||||||
| NOR | 
|
| |||||||||||||||||||||
| XOR | 
|
|
|||||||||||||||||||||
| XNOR | 
|
| |||||||||||||||||||||
قواعد المنطق البوليني
[عدل]مع مراعاة أن المتغيرات z,x,y قيمتهما إما 0 أو 1:
البوابات المنطقية الأساسية
[عدل]تتألف البوابات المنطقية بشكل عام من ثلاثة بوابات أساسية (AND-OR-NOT).
التابع المنطقي AND
[عدل]يعبر عن التابع and بالعلاقة التالية(Z=A AND B)والسبب في هذه التسمية هو أن Z=TRUE فقط حينما يكون كلا من (AوBحقيقيان)
وجدول الحقيقة للتابعAND هو:
| P | Q | |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
يعبرعن التابع AND بشكل آخر باستخدام العلاقة التالية:Z=A.B والتي تكتب بشكل أبسط كما يلي:Z=AB تظهر العلاقتان السابقتان أن Zهو الناتج من عملية ضرب AوB وبالطبع ليس المقصود هنا الضرب الحسابي كما أن AوB ليسا بعددين
صفات التابعAND
[عدل]- إن أول صفة للتابع AND هي قابليته للتبديل، أي تغيير ترتيب AوB لا يؤثر على التابع Zكما هو مبين بالعلاقة:Z=AB=BA
ويمكن التأكد من صحة هذه العلاقة بتبديل موضعي العمودين AوB في جدول الحقيقة
و التأكد من عدم تغيير القيم الموجودة في العمود Z
- إن الصفة الثانية للتابع AND هي قابليته للتجميع أي إذا كانت هناك ثلاث متحولات
Aو BوC فبغض النظر عن ترتيب عمليات الجدول لهذه المتحولات لا تتغير قيمة التابع
Z أي:Z=A(BC)=(AB)C
تمثل الدائرة التي تشكل الجدول المنطقي Z=AB بواسطة الرمز التالي:
وبسبب خاصية الانتقال والتجميع للتابع AND تمثل الدارة التي تشكل الجداء المنطقي
لعدة متحولات بواسطة
التابع المنطقي OR
[عدل]يعبر عن تابع OR بالعلاقة التالية: Z=A OR Bوالسبب في هذه التسمية هو
أن(Z=TRUE) إذا كان(A=T)أو(B=T)أو إذا كان كلا من AوBحقيقيان.
وجدول الحقيقة للتابعOR هو:
ويمكن كتابة التابع OR بشكل آخر كما يلي: Z=A+B
بالطبع إشارة الجمع هناك لا تعني عملية الجمع الحسابية وفي كثير من الأحيان يسمى
التابع (A+B)بالمجموع المنطقي ل(A وB)
صفات التابع OR
[عدل]- إن التابع OR كالتابع AND يتمتع بصفة التبديل والتجميع التي يمكن التعبير
عنهما بالعلاقتين التاليتين:
Z=A+B=B+A
Z=A+(B+C)=(A+B)+C
تمثل الدارة التي تشكل المجموع المنطقي Z=A+B من أجل متحولين :
ومن أجل عدة متحولات:
ثالثا:التابع NOT (النفي والانعكاس):
العاكس بالتعريف هو بوابة منطقية بمدخل واحد ومخرج واحد.حيث الخرج متمم
للدخل حتما. فحينما يكون الدخل حقيقيا يكون الخرج غير حقيقيا وبالعكس أي حينما
يكون الدخل مساويا ل(A)يكون الخرج Z=A' وجدول الحقيقة للتابع NOT هو:
يستخدم لتمثيل العاكس الرمز التالي:
ويمكن من هذه التوابع الثلاث تشكيل بعض التوابع الفرعية مثل التابعين المنطقيين
حيث يعتبر التابع NANDمتمما للتابع AND أي
NAND و NOR وذلك من التابعين الأساسيين ORو AND
(Z=(A.B)'=NOT(A AND B
لذا يمكن تمثيل بوابة NAND باستخدام بوابة AND وتوضع دائرة النفي على
خرج هذه البوابة كما هو مبين بالشكل:
كذلك التابع NOR يعتبر متمما للتابع OR أي:
(Z=(A+B)'=NOT(A OR B
وكذلك تمثيله باستخدام بوابة OR ووضع دائرة النفي على مخرج هذه البوابة كما هو
مبين بالشكل:
تتصف عمليتي NANDوNOR بأنهما قابلتين للتبديل أي أن:
'Z=AB'=BA
'(Z=(A+B)'=(B+A
ولكنهما غير قابلتين للتجميع.
انظر أيضًا
[عدل]- منطق رياضي
- دارة المقارن
- تاريخ الأجهزة الحاسوبية (ستينيات القرن العشرين-الآن)
- ارتداد أرضي
- أجهزة منطقية قابلة للبرمجة
- بوابة اكس اور
- تكافؤ منطقي
المراجع
[عدل]- ^ Family Specifications - HCMOS family characteristics, Philips Semiconductors 1988 - sur mit.edu نسخة محفوظة 2024-07-07 على موقع واي باك مشين.
- ^ Initiation à la micro-informatique, C. Tavernier - Le Haut-Parleur n°1676 janvier 1982, page 162 - archivé sur archive.org
- ^ Aide-mémoire Composants électroniques 3e édition, P. Mayé - page 148 - archivé sur archive.org
- ^ Brown، Stephen D.؛ Francis، Robert J.؛ Rose، Jonathan؛ Vranesic، Zvonko G. (1992). Field Programmable Gate Arrays. Boston, MA: Kluwer Academic Publishers. ISBN:978-0-7923-9248-4. مؤرشف من الأصل في 2016-12-04. اطلع عليه بتاريخ 2012-11-28.
- ^ PDF Eprint. نسخة محفوظة 17 أكتوبر 2017 على موقع واي باك مشين.
- ^ Bostock، Geoff (1988). Programmable logic devices: technology and applications. New York: McGraw-Hill. ISBN:978-0-07-006611-3. مؤرشف من الأصل في 2017-10-11. اطلع عليه بتاريخ 2012-11-28.



























