من ويكيبيديا، الموسوعة الحرة
مقلوب المعاوقة أو ثنائية المعاوقة هو أحد المصطلحات المستخدمة في تحليل الدوائر الكهربية، حيث أن مقلوب المعاوقة
Z
{\displaystyle Z}
Z
′
=
1
Z
{\displaystyle Z'={\frac {1}{Z}}}
Z
{\displaystyle Z}
Y
′
=
Z
{\displaystyle Y'=Z}
وهذا يتفق مع فكرة الازدواجية في الدوائر الكهربائية، حيث:
Z
=
V
I
{\displaystyle Z={\frac {V}{I}}}
Z
′
=
I
V
{\displaystyle Z'={\frac {I}{V}}}
[ 1]
[ عدل ]
[ 2]
العنصر
Z
ثنائي العنصر
Z'
المقاوم الكهربي R
R
{\displaystyle R\,\!}
الموصل الكهربي G = R
1
R
{\displaystyle {\frac {1}{R}}}
الموصل الكهربي G
1
G
{\displaystyle {\frac {1}{G}}}
المقاوم الكهربي R = G
G
{\displaystyle G\,\!}
الملف L
i
ω
L
{\displaystyle i\omega L\,\!}
المكثف C = L
1
i
ω
L
{\displaystyle {\frac {1}{i\omega L}}}
المكثف C
1
i
ω
C
{\displaystyle {\frac {1}{i\omega C}}}
الملف L = C
i
ω
C
{\displaystyle i\omega C\,\!}
معاوقات على التوالي Z = Z1 + Z2
Z
1
+
Z
2
{\displaystyle Z_{1}+Z_{2}\,\!}
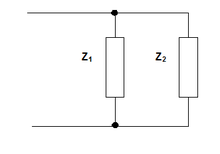
معاوقات على التوازي Y = Z1 + Z2
1
Z
1
+
Z
2
{\displaystyle {\frac {1}{Z_{1}+Z_{2}}}}
معاوقات على التوازي 1/Z = 1/Z1 + 1/Z2
Z
=
Z
1
Z
2
Z
1
+
Z
2
{\displaystyle Z={\frac {Z_{1}Z_{2}}{Z_{1}+Z_{2}}}}
معاوقات على التوالي 1/Y = 1/Z1 + 1/Z2
1
Z
1
+
1
Z
2
{\displaystyle {\frac {1}{Z_{1}}}+{\frac {1}{Z_{2}}}}
مصدر جهد كهربي V
V
{\displaystyle V\,\!}
مصدر تيار كهربي I = V
I
{\displaystyle I\,\!}
مصدر تيار كهربي I
I
{\displaystyle I\,\!}
مصدر جهد كهربي V = I
V
{\displaystyle V\,\!}
هناك طريقة بيانية أسهل في الاستخدام من التعبير الرياضي:
توصيل مصدر الجهد الكهربي بين كل عقدتين في الدائرة، والغرض من هذه العملية هو حفظ العقد من الضياع عند تحويل الدائرة.
رسم نقطة داخل كل شبكة من الشبكات في الدائرة Z، هذه النقاط سوف تصبح عقد الدائرة Z'.
يتم رسم مصدر تيار كهربي بين كل نقطة داخل الشبكة وبين مصدر الجهد الكهربي في الدائرة Z.
يتم رسم ثنائية المعاوقة Z' بين العقد في الدائرة الجديدة Z'.[ 3] ثنائية المعاوقة لدائرة على شكل واي من ثلاث ملفات يعطي دائرة على شكل دلتا من ثلاث مكثفات.
دائرة على شكل حرف واي من ثلاث ملفات توصيل مصدر الجهد الكهربي بين كل عقدتين في الدائرة رسم نقطة داخل كل شبكة
يتم رسم مصدر تيار كهربي بين كل نقطة داخل الشبكة وبين مصدر الجهد الكهربي في الدائرة Z، ثم رسم ثنائية المعاوقة Z' بين العقد في الدائرة الجديدة. دائرة ثنائية المعاوقة Z' حذف مصادر التيار الكهربي
^ Ghosh, Smarajit, Network Theory: Analysis and Synthesis , Prentice Hall of India, pp.50-51
^ Guillemin, Ernst A., Introductory Circuit Theory , New York: John Wiley & Sons, 1953, pp.535-539
^ Guillemin, pp.49-52
أشهر التمثيلات المستخدمة أشخاص مفاهيم مرتبطة تطبيقات