حوسبة كمومية

حساب كمومي

صنف فرعي من	الحوسبة
المواضيع	حاسوب كمومي — تفوق كمومي
التاريخ	الخط الزمني للحوسبة الكمومية والاتصالات الكمومية

كرة بلوخ هي أحد تمثيلات بت كمومي (الكيوبت)، الوحدة الأساسية للحوسبة الكمومية.

الحوسبة الكمومية (بالإنجليزية: Quantum computing)‏ هو أي وسيلة تعتمد على مبادئ ميكانيكا الكم وظواهره، مثل حالة التراكب الكمي والتشابك الكمي، للقيام بمعالجة البيانات. في الحواسيب التقليدية، تكون كمية البيانات مقاسة بالبت: أما في الحاسوب الكمي فتقاس كمية البيانات ببت كمومي أو (الكيوبت QuBit) (اختصارا لـ Quantum bits). المبدأ الأساسي للحوسبة الكمية هي القدرة على الاستفادة من الخواص الكمية للجسيمات لتمثيل البيانات ومعالجتها، إضافة لاستخدام قواعد ميكانيكا الكم لبناء وتنفيذ التعليمات والعمليات على هذه البيانات.

التاريخ

منذ ظهور أول حاسوب ميكانيكي عامَ 1941م، حدثت العديد من الاكتشافات والاختراعات الفيزيائية التي غيرت وجه عالم الحواسيب وصنعت منها الأجهزة الحديثة والمتطورة التي نراها اليوم. ومن أهم هذه الاختراعات والاكتشافات الفيزيائية هي: الأنابيب المفرغة، الترانزستورات والدوائر المتكاملة.

تطورت الحواسيب في اتجاهات مختلفة، كما أنها أصبحت صغيرة الحجم، خفيفة الوزن، جميلة المظهر، متطورة وذات كفاءة عالية مقارنةً بالحواسيب القديمة ذات أحجام كبيرة (بحجم الغرفة تقريباً)، واستخدمت تقنية الأنابيب المفرغة الإلكترونية مما أكسبها كفاءة متدنية جدا مقارنةً مع أي حاسوب شخصي في أيامنا هذه.

حاليا تجرى الأبحاث على كلا الجانبين: البرمجيات والمكونات الصلبة للحواسيب. فحتى هذه اللحظة ما زال علينا حمل حواسيب محمولة تزن عدة كيلوغرامات، استخدام لوحة المفاتيح، إعادة تكرار الأوامر والإجابة على أسئلة بسيطة يطرحها الحاسوب. (الشكل 1.2 يظهر حاسوباً تقليدياً من النوع المعروف باسم الحواسيب الشخصية. ولكن معضلات أخرى ما زالت موجودة. مثلاً البنوك، كبرى الشركات، وحتى الحكومات دائماً في حالة قلق من اختراق بياناتها المحوسبة وكسر سريتها، مما يكلفها أمولا طائلة للتشديد من سرية المعلومات، ولكن قراصنة الحاسوب أيضا يتطورون يوما عن يوم. تحليل الأرقام الكبيرة إلى عواملها الأولية يمثل تحدياً آخر لعلماء الرياضيات. فمثلاً لتحليل رقم يتكون من 230 رقماً ستتطلب هذه العملية ملايين السنين عن طريق أحدث الحواسيب الكلاسيكية. حواسيب الكم ربما تمثل حلاً لمثل هذه المعضلات. أو بمعنى آخر نستطيع القول أن حواسيب الكم أعلى كفاءة من الحواسيب الكلاسيكية. إذن؛ ما هي حواسيب الكم؟ كيف تختلف عن الحواسيب الكلاسيكية؟ وما المتوقع منها بالضبط؟

IBM Q System One (2019)، أول حاسوب كمومي تجاري صغير

فمثلا، حسابات الأحوال الجوية وتغيراتها اليومية، ومن ساعة إلى ساعة، تحتاج لبيانات كثيرة جدا تأتي من مختلف البلاد والمناطق، وهي عبارة عن قياسات تتعلق بدرجات الحرارة والضغط الجوي ونسب الرطوبة وحالة الأوزون، وغيرها من قياسات مستمرة؛ معالجة هذا القدر الكبير من البيانات، ومحاولة استباط والتنبؤ بما سيكون عليه الطقس في الساعات القادمة، كل ذلك يحتاج إلى حواسيب ضخمة للتعامل معها واصدار النتائج أولا بأول بصفة مستمرة. وتشكل الحواسيب الكمومية حلا لهذا العمل الكبير.

في العام 1994م أعلن عالم الرياضيات بيتر شور عن اكتشافه لخوارزمية بسيطة لتحليل الأرقام إلى مكوناتها الأولية، بواسطة آلة حاسوبية تقوم على أسس فيزياء الكم. ومنذ ذلك الوقت ما انفكت الأبحاث تحاول إنتاج حاسوب كمومي فعال قابل للاستخدام كحواسيب اليوم بكفاءة مضاعفة. لذا لابد أن يكون الحاسوب الكمومي من مكونات إلكترونية صغيرة جداً تماثل الذرات المنفردة حجماً. وبالتالي ستخضع هذه المكونات متناهية الصغر لقوانين ميكانيكا الكم موفيةً بذلك الشرط اللازم لعمليات الحاسوب الكمي. ولهذا السبب يعتبر الحاسوب الكمي جزءاً من تقنية النانو الحديثة التي تتعامل مع الأنظمة التي تحتوي علي مكونات نانوية الأبعاد (أجهزة ذات حجم ~ 1 نانو متر = ⁹^-10 من المتر).

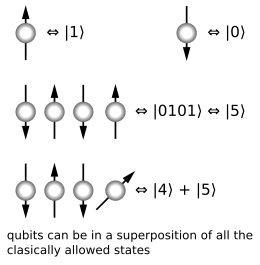
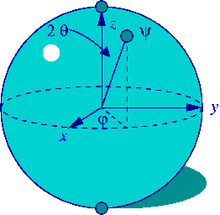
في حين أن وحدة المعلومات في الحواسيب الكلاسيكية هي البت، يعتبر البت الكمومي وحدة المعلومات في الحواسيب الكمومية. بت واحد يعادل إحدى حالتين 0 أو 1 واللذان يمثلان النظام الثنائي الذي تتعامل معه الحواسيب الكلاسيكية. بينما يستطيع البت الكمومي أن تمثل بالإضافة إلى هاتين الحالتين حالة التراكب الكمي المكونة منهما معا؛ وبالتالي فان زوجاً من البت الكمية بستطيع أن يمثل أي تراكب كمي من الحالات الأربعة: I0,0>, I0,1>, I1,0> or I1,1> حيث نستخدم طريقة ديراك لتمثيل الحالة الكمية. عموما فالحاسوب الكمي المكون من n بت كمية يمكن أن يكون أي تراكب اعتباطياً من 2n حالة مختلفة متواجدين آنيا، بينما في الحواسيب العادية n عدد من البتات يعني n حالة محددة ولا توجد أي حالات متزامنة آنياً. وهذا يعكس القوة الحوسبية الكبيرة التي تقدمها الحواسيب الكمية مقارنةً بالحواسيب التقليدية.

الحواسيب الكمية ما تزال قيد التطوير والبحث، وما يزال الجدل قائماً حول ما إذا كان إيجاد مثل هذه الحواسيب على أرض الواقع في المستقبل ممكناً أو لا. وعلى كل حال فإن العمل على الحواسيب الكمية، يستطيع إثراء فيزياء الكم الأساسية، كما يستطيع إثراء الأبحاث على مستوي القياس النانوي. وتم إنتاج حاسوب كمي صغير مكون من سبعة بتات كمية، مثلت بواسطة سبعة مغازل نووية (nuclear spins)، خمسة منها من نويات الفلور، واثنان من نويات الكربون -13 (انظر الشكل1.3)، وذلك في معامل آي بي إم وستانفورد.

فبشكل مماثل لقضيب مغنطيسي يشير إلى الشمال أو الجنوب، يستطيع كل مغزل أن يمثل الأرقام الثنائية "0" أو "1" أو كلاهما معاً (انظر إلى الأسهم السوداء في الشكل 1.3). ويمكن التحكم في ذلك عن طريق مجالات مغنطيسية وموجات الراديو (تقنية الرنين المغنطيسي النووي). وبواسطة حاسوب كمومي ذي سبع بتات الكمية، أمكن الاستفادة من ميزة الحوسبة الكمية الفريدة، ألا وهي قابلية التراكب، لقياس الأعداد الأولية المكونة للرقم 15 ألا وهي 3 و 5. ولكن تحليل الأعداد الكبيرة إلى عواملها الأولية يتطلب حاسوباً ذو عدد أكبر من البتات الكمية، ويبقى هذا تحدياً لبناء حاسوب كمي حقيقي كبير.

آلة تورنغ

آلة تورنغ والتي وضعها آلان تورنغ في ثلاثينيات القرن العشرين، هي آلة نظرية تتألف من شريط لانهائي الطول مُقسم إلى مربّعات صغيرة، كل من هذه المربّعات يَحمل الرمز 1 أو 0 أو يبقى فارغاً. يقوم جهاز (قراءة/كتابة) بقراءة هذه الرموز والفراغات وهذا ما يعطي الآلة التعليمات لتقوم بعملٍ ما. الآن في آلة تورنغ الكمومية الفرق أنّ الشريط ورأس (القراءة/كتابة) يوجد في حالةٍ كمومية وهذا يعني أنّ الرموز على الشريط يمكن أن تكون 0 أو 1 أو حالة مُختلطة من 0 والـ 1. بعبارة أخرى الرموز تكون 1 و 0 و كل النقط بينهما في نفس الوقت. فبينما تقوم آلة تورنغ العادية بتنفيذ عملية واحدة في وقت واحد، تقوم آلة تورنغ الكمومية بتنفيذ العديد من العمليات في نفس الوقت. تعمل حواسيب اليوم –كآلة تورنغ- بمعالجة البيتات الموجودة في حالتين 0 أو 1. الحواسيب الكمومية ليست مُقيّدة بحالتين فهي تُرمز المعلومات على شكل بيتات كمومية أو اختصاراً (QuBits) والتي يمكن أن توجد في الحالة المختلطة. يمكن تمثّيل البتات الكمومية عبر: ذرّات، أيونات، فوتونات أو إلكترونات والأجهزة التي تتحكّم بها والتي تعمل معاً فتصبح ذاكرةً أو معالجاً. لأنّ الحواسيب الكمومية تحوي هذه الحالات المُتعددة وبنفس الوقت، فهي تملك القدرة على أن تكون أقوى بملايين المرات من الحواسيب الفائقة الموجودة اليوم.

التحكم بالحواسيب الكمومية

يتحكم علماء الحواسيب بالأجزاء المجهرية التي تتصرف كبتات كمومية في الحواسيب الكمومية مستخدمين أجهزة تحكم:

• لاقط الأيونات: يستخدم حقل ضوئي أو مغناطيسي (أو مزيج من الإثنين) لالتقاط الأيونات.

• اللاقطات الضوئية: تستخدم الأمواج الضوئية لتتحكم بالجزيئات.

• النقط الكمومية: تصنع من مواد نصف ناقلة وتستخدم لاحتواء الإلكترونات والتلاعب بها.

• أنصاف نواقل مشوبة: تحوي الإلكترونات باستخدامها ذرات “غير مطلوبة” موجودة في المواد نصف الناقلة.

• دارات فائقة النقل: تسمح للإلكترونات بالتدفق دون أية مقاومة تقريبًا، وعند درجات حرارة منخفضة.

التطبيقات المحتملة للحوسبة الكمومية

علم التشفير

أحد أهم تطبيقات الحوسبة الكمومية المحتملة هو تمكنها من كسر أنظمة التشفير قيد الاستخدام حاليا. تعتمد أنظمة التشفير الحالية على الإعتقاد بأن الحواسب الشائعة لا يمكنها تحليل عدد صحيح كبير إلى عوامله الأولية، لو كان هذا العدد هو حاصل ضرب عدد قليل من الأعداد الأولية (مثلا، لو كان العدد هو حاصل ضرب عددين أوليين كل منهما يتكون يحتوي على 300 خانة). غير أن الحاسوب الكمومي يمكنه حل هذه المشكلة بكفاءة بتطبيق خوارزمية شور للحصول على عوامل العدد الكبير. وهذه القدرة ستمكن الحاسوب الكمومي من كسر العديد من أنظمة التشفير قيد الاستخدام حاليا، حيث أنه سيكون لدينا حينها خوازرمية تتطلب وقت متعدد الحدود (كدالة في عدد خانات الرقم) لحل المسألة. إن لائحة أنظمة التشفير المهددة بالكسر تشمل: خوارزمية آر إس إيه، وتبادل مفتاح ديفي-هيلمان، وخوارزمية المنحنى الإهليجي لديفي هيلمان. وهذه الخوارزميات كلها تُستخدم حاليا لتأمين صفحات الإنترنت وتشفير البريد الإلكتروني والكثير من أنواع البيانات الآخرى، لذا فإن كسرها ستكون له عواقب معتبرة فيما يتعلق بالأمان والخصوصية الإلكترونية.

مهمات البحث

وأيضا من أكثر التطبيقات المعروفة للحواسب الكمومية هو مهمة «البحث غير الممنهج» (unstructured search)، وهي مهمة البحث عن عنصر معين في لائحة تتضمن عدد $n$ من العناصر. هذه المهمة يمكن القيام بها بواسطة خوارزمية جروفر بإستدعاء عدد $O({\sqrt {n}})$ من الطلبات. وهذا العدد من الطلبات هو أقل تربيعيا من الطلبات $\Omega (n)$ التي تتطلبها الخوارزميات الكلاسيكية. وهذه ليست فقط ميزة أفضل للحواسب الكمومية، بل أنها أفضل الحلول المحتملة على الإطلاق، حيث بُرْهِنَ على أن خوارزمية جروفر تعطي أقصى إحتمالية ممكنة للعثور على العنصر المطلوب.

محاكاة النظم الكمومية

أنظمة المحاكاة الكلاسيكية عاجزة عن محاكاة التركيبات الكمومية بالكون، مثل الذرات والجزيئات وكل ما يتعلق بعلوم الكيمياء والتقنية النانوية، بشكل فعال. ولهذا يؤمن الكثيرون بأن الحوسبة الكمومية هي الحل لمحاكاة هذه التركيبات. والحوسبة الكمومية قادرة أيضا على محاكاة الذرات والجزيئات في ظروف غير عادية، مثل التفاعلات التي تتم بداخل مصادم جسيمات.

انظر أيضًا

• نظام IBM كوانتم سيستم ون
• ميكانيكا الكم
• بت كمومي
• حوسبة ضوئية
• نظرية الألعاب الكمومية
• خط زمني للحوسبة الكمومية
• دائرة كمومية