رسم زائدي

في الرياضيات، المخطط الزائدي أو الرسم الزائدي (بالإنجليزية: Hypergraph) هو تعميم لمفهوم الرسم البياني أو المخطط والذي كل ضلع فيه يحتوي على عدد من الرؤوس. بصيغة رياضية، الرسم الزائدي هو الزوج المرتب حيث هي مجموعة من العناصر التي تسمى رؤوس، والمجموعة هي مجموعة غير خاليه جزئيه من . عناصر المجموعة تسمى أضلاع زائديه أو أضلاع. بالتالي هي مجموعة غير خاليه من مجموعة القوه . حجم مجموعة الرؤوس يسمى رتبة الرسم الزائدي بينما حجم مجموعة الاضلاع يسمى حجم الرسم الزائدي.
في حين أن أضلاع الرسم البياني يحتوي على عنصرين فقط من مجموعة الرؤوس، الأضلاع الزائدية هي مجموعات مختارة من الرؤوس، ومن الممكن أن تحتوي على أي عدد من الرؤوس. لكن الغالب يرغب بدراسة الرسوم الزائديه التي كل أضلاعها تحتوي على نفس العدد من الرؤوس. الرسم الزائدي ذو أضلاع موحدة السعة (k-uniform hypergraph) هو الرسم الزائدي الذي كل ضلع زائدي به من الرؤوس، أو بمعنى آخر هو الرسم الزائدي الذي أضلاعه الزائدية هي مجموعات بها من الرؤوس. فبالتالي، الرسم الزائدي ذو اضلاع سعتها 2 هو الرسم البياني المعروف، والرسم الزائدي ذو الاضلاع الموحدة بسعة 3 هو مجموعة من المجموعات الثلاثية، أي بها 3 عناصر. الرسم الزائدي يسمى أيضاً بنظام المجموعة أو عائلة من المجموعات والمستوحاة من مجموعة شاملة.
الرسومات الزائدية يمكن اعتبارها كهياكل الوقوع (incidence structures). وبصورة خاصة، يوجد مخطط وقوع ثنائي التجزئة (incidence graph" or Levi graph ) مقابل كل رسم زائدي. بالمقابل، ليس كل الرسومات البيانية الثنائية التجزئة يمكن اعتبارها كرسومات وقوع لرسومات زائدية.
المخططات الزائدية لها مسميات عديدة. ففي الهندسة الحاسوبية يسمى المخطط الزائدي في بعض الاحيان بـ range space وبالتالي أضلاعه الزائدية تسمى ranges.[1] تسمى الرسوم الزائديه في نظرية اللعب التعاوني بالألعاب البسيطة وينطبق نفس المسمى لحل المشاكل في نظرية الإختيار الإجتماعي. تسمى الأضلاع الزائدية في بعض الدراسات بالروابط الزائدية (hyperlinks) أو موصلات (connectors).[2]
يوجد أنواع خاصة من الرسومات الزائدية والمصنفه حسب سعة الأضلاع الزائديه بها. فمثلا الرسم الزائدي من السعة كما وضح أعلاه. ورسم زائدي اخر يسمى clutters والذي به كل ضلع زائدي ليس محتوى بأي ضلع زائدي آخر بنفس الرسم الزائدي. بالمقابل، الرسومات الزائديه التي تحتوي على كل المجموعات الجزئية من أي ضلع زائدي بها تسمى بـ abstract simplicial complexes.
مصطلحات[عدل]
تعاريف[عدل]
يوجد أنواع مختلفه من الرسوم الزائديه، منها[عدل]
- الرسم الزائدي الخالي: والذي لايحتوي على أي ضلع زائدي.
- الرسم الزائدي المتعدد أو الغير بسيط: وهو الرسم الزائدي الذي ممكن ان يحتوي على عروة أو اضلاع مكرره وهو عباره عن ضلعين يحتويان على نفس مجموعة الرؤوس.
- الرسم الزائدي البسيط وهو رسم زائدي لايحتوي على عروات ولا أضلاع مكررة.
- الرسم الزائدي المنتظم ذو الدرجة (regular hypergraph-): هو رسم زائدي الذي كل كل رأس به له نفس الدرجة .
يوجد عدة مصطلحات للمصطلح المقابل لـ الرسم الجزئي في الرسم الزائدي لأن أضلاع الرسم الزائدي ممكن أن تحتوي على أي عدد من الرؤوس. من هذه المسميات يعرف بالرسم الزائدي الثانوي (subhypergraphs) والرسم الزائدي الجزئي (partial hypergraphs) و section hypergraphs وسيتم تعرف كل من هذه المصطلحات كما موضح أدناه.
- ليكن رسم زائدي مكون من الرؤوس ولديه مجموعة الأضلاع
حيث و هما مجموعتي الترميز index sets للرؤوس والأضلاع على التوالي.
الرسم الزائدي الثانوي (subhypergraphs) من الرسم الزائدي هو رسم زائدي مأخوذ من مع حذف بعض الرؤوس. بصيغة رياضية، الرسم الزائدي الجزئي المولد بواسطة معرف كالآتي:
توسعة (extension) الرسم الزائدي الثانوي هو رسم زائدي حيث كل ضلع من هو محتوى جزئيا بالرسم الزائدي الثانوي ومحتوى كليا في التوسعة . رياضيا:
حيث و .
الرسم الزائدي الجزئي هو رسم زائدي من مع حذف بعض الآضلاع الزائديه. بصيغه رياضية، ليكن مجموعة جزئية من مجموعة ترميز الآضلاع٫ الرسم الزائدي الجزئي المولد بالمجموعة هو رسم زائدي .
لتكن مجموعة معطاه، يعرف section hypergraph بآنه رسم زائدي جزئي معرف كالتالي:
.
الرسم الزائدي المزدوج (dual hypergraph) للرسم الزائدي هو رسم زائدي مجموعة رؤوسه هي وآضلاعه معطى بالمجموعة حيث .
لاحظ آن الرسم الزائدي المزدوج لـ هو ٫ آي آن .
نمذجة المخطط ثنائي التجزئة[عدل]
يمكن تمثيل آي رسم زائدي برسم ثنائي التجزئة كما يلي: المجموعات و تمثل تجزئات لـ و هو ضلع في إذا وفقط إذا كان كل رأس ينتمي للضلع الزائدي في . بالمقابل ليس كل رسم ثنائي تجزئة تمثل رسم زائدي. يسمى هـذا الرسم الثنائي برسم الوقوع .
بدون دورة (Acyclicity)[عدل]
يوجد عدة مصطلحات غير متكافئة للرسومات الزائديه بدون دورات ٫ بعكس الرسم الغير موجه والذي به تعريف موحد للدورات وللرسومات بدون دورات.
عرف العالم بيرج (Claude Berge) آول تعريف للرسومات الزائديه بدون دورات:[3] يكون الرسم الزائدي هو رسم خالي من الدورات إذا كان رسم الوقوع المقابل له لايحتوي على أي دورة. هذا التعريف يعتبر محدود جداً٫ فعلى سبيل المثال إذا كان الرسم الزائدي يحتوي على زوج من الرؤوس المختلفة وزوج من الآضلاع الزائديه المختلفة بحيث آن و فإنه يمكن اختبار انه لايحتوي على دوره بزمن خطي بواسطة رسم الوقوع له.يوجد تعريف آخر المسمى ب α-acyclicity آضعف ومختلف من تعريف بيرج.[4]
يمكن بزمن خطي تحديد ماإذا كان أي رسم زائدي هو α-acyclicity.[5]
التشاكل والمساواة[عدل]
تشاكل رسوم زائدي هو داله من مجموعة رؤوس رسم زائدي إلى مجموعة رؤوس رسم زائدي آخر بحيث كل ضلع هو صوره لضلع بالرسم الزائدي المقابل.
الرسم الزائدي هو تشاكل احادي للرسم الزائدي ونكتب إذا كان يوجد تقابل وتبديله لـ بحيث آن . بالتالي تسمى دالة التقابل في هذه الحالة بتشاكل احادي للرسومات. لاحظ ان إذا وفقط إذا كان .
أمثلة[عدل]
ليكن لدينا الرسم الزائدي والذي مجموعة أضلاعه حيث
.
والرسم الزائدي والمعرف بمجموعة أضلاعه حيث
.
بالتالي فإن الرسمين الزائدين و متشاكلان حيث الدالة معرفه كالتالي:
.
هذين الرسمين متشاكلان لكن ليس تشاكل قوي (strongly isomorphic) لأنه يوجد رأس في ينتمي للأضلاع أي أن
لكن لايوجد رأس في بحيث ينتمي للأضلاع لأن .
في هذا المثال الرسمين الزائدين و متكافئين ونكتب في هذه الحالة . أيضا رسومهم المزدوجه متشاكله٫ أي أن .
الرسوم الزائديه المتماثله[عدل]
رتبة (rank) رسم زائدي ويرمز له بالرمز هو أكبر سعة لآي من اضلاع الرسم الزائدي. يسمى الرسم الزائدي الذي كل ضلع فيه يحتوي على نفس العدد من الرؤوس مساوي للعدد بالرسم الزائدي الموحد السعه ٫ ويسمى أيضا hypergraph-. بالتالي فإن الرسم هو عباره عن رسم زائدي من السعه .
درجة الرآس ويرمز له بالرمز هي عدد الاضلاع التي تحتوي على هذا الرآس. يسمى الرسم الزائدي بمنتظم من الدرجة (regular-) إذا كان درجة كل رآس فيه تساوي .
الرسم الزائدي المزدوج لرسم زائدي موحد السعه هو منتظم والعكس صحيح.
القواطع (Transversals)[عدل]
يٍُعرف قاطع رسم زائدي بالمجموعة التي تتقاطع مع كل ضلع في بمجموعه غير خالية من الرؤوس. يطلق على بآنه القاطع الآصغر إذا كان لايوجد أي مجموعه جزئيه فعليه من وتمثل قاطع. الرسم الزائدي القاطع (transversal hypergraph) للرسم الزائدي هو رسم زائدي والذي مجموعة آضلاعه تحتوي على كل القواطع الصغرى لـ .
يوجد تطبيقات لحساب الرسم الزائدي القاطع في امثلة التراكيب وفي نظرية الألعاب وفي عدة فروع من علوم الحاسب على سبيل المثال في التعلم الألي وفهرسة قواعد البيانات وتنقيب البيانات وأمثلية البرمجيات وsatisfiability problem.
مصفوفة الوقوع (Incidence matrix)[عدل]
لتكن مجموعة الرؤوس و مجموعة الآضلاع الزائديه. كل رسم زائدي له مصفوفة وقوع من النوع حيث:
يمثل منقول مصفوفة الوقوع الرسم الزائدي المزدوج لـ .
مسألة تلوين الرسوم الزائدية (Hypergraph coloring)[عدل]
في تلوين الرسم الزائدي التقليدي٫ يتم تعيين لون واحد من ألوان المجموعة لكل رأس بالرسم الزائدي بحيث أن أي ضلع زائدي يحتوي على الأقل رأسين بألوان مختلفه. بمعنى آخر، لايمكن الحصول على ضلع بلون واحد فقط وبه على الأقل رأسين. هذا التعريف هو تعميم مباشر لتلوين الرسومات. يسمى أصغر عدد من الألوان المختلفه والممكن استخدامها بتلوين رسم زائدي يسمى بـ chromatic number للرسم الزائدي.
الرسومات الزائديه التي يوجد بها عالأكثر من الألوان تُلقب بـ k-colorable. الرسومات الزائديه ثنائي التلوين (2-colorable) هي رسوم زائديه ثنائية التجزئة.
يوجد العديد من التعاريف والتي تعمم مسألة تلوين الرسوم الزائديه. أحد هذه التعاريف التي تسمى بمسألة تلوين مختلط للرسم الزائدي (mixed hypergraph coloring) والتي تسمح بوجود أضلاع موحدة اللون. يوجد رسوم زائديه غير قابله للتلوين لأي عدد من الألوان. بمسألة التلوين المختلط وعندما يكون الرسم الزائدي قابل للتلوين فإن أصغر وأكبر عدد مستخدم من الألوان تُعتبر على التوالي حد سفلي وعلوي لـ chromatic number .
التجزئات (Partitions)[عدل]
نظريات[عدل]
تمثيل الرسم الزائدي[عدل]
Hypergraph grammars[عدل]
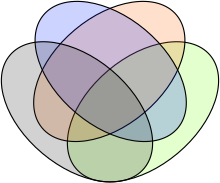
تعميمات[عدل]
تدريس الرسم الزائدي[عدل]
المزيد[عدل]
مراجع[عدل]
- ^ Haussler، David؛ Welzl، Emo (1987)، "ε-nets and simplex range queries"، Discrete and Computational Geometry، ج. 2، ص. 127–151، DOI:10.1007/BF02187876، MR:0884223
- ^ Judea Pearl, in HEURISTICS Intelligent Search Strategies for Computer Problem Solving, Addison Wesley (1984), p. 25.
- ^ Claude Berge, Graphs and Hypergraphs
- ^ C. Beeri, R. Fagin, D. Maier, M. Yannakakis, On the Desirability of Acyclic Database Schemes
- ^ R. E. Tarjan, M. Yannakakis. Simple linear-time algorithms to test chordality of graphs, test acyclicity of hypergraphs, and selectively reduce acyclic hypergraphs. SIAM J. on Computing, 13(3):566-579, 1984.
ملاحظات[عدل]
| رسم زائدي في المشاريع الشقيقة: | |
| |










































































