جداء نقطي
المظهر
(بالتحويل من الضرب القياسي)
الجداء النقطي[1] أو الضرب النقطي أو الجداء القياسي أو الضرب القياسي أو الجداء السُّلَّمِيّ[2] (بالإنجليزية: Dot product) هو عمليةٌ جبرية بين متجهين ونتيجتها كمية قياسية.
تعريف
[عدل]تعريف جبري عام
[عدل]ليكن فضاء متجهي حقيقي (معرف على حقل الأعداد الحقيقية )
نعرف الجداء السُلمي على أنه كل دالة :
تعريف على
[عدل]الضرب القياسي الاعتيادي لمتجهتين و من يعرف ويرمز له بـ [3]
- على سبيل المثال، في الفضاء ثلاثي الأبعاد ، الضرب القياسي لمتجهين و هو :
تعريف هندسي
[عدل]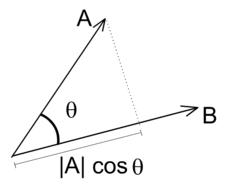
في الفضاء الإقليدي، صيغة أخرى لحاصل الضرب القياسي
حيث A هو طول المتجه A وB هو طول المتجه B وθ هي الزاوية المحصورة بينهما.
خصائص
[عدل]- تبديلي :
- تنبثق هذه الخاصية من تعريف الجداء القياسي (θ هي الزاوية المحصورة بين a وb)
- توزيعي على جمع المتجهات : (a.b + a.c = a.(b+c
- تعامدي : متجهتان a وb مختلفتان عن الصفر يكونان متعامدتين إذا وفقط إذا توفر a.b = 0.
- لا إلغاء :
تطبيق لقانون الجيب التمام
[عدل]
وهذا هو قانون الجيب التمام. وتعبر أيضا عن خاصية الكاشي
في الفيزياء
[عدل]الجداء القياسي يعبر عن كميات عددية لا علاقة لها برسم شعاع مثل (الجهد، العزم ....)
تعميمات
[عدل]الجداء الداخلي
[عدل]انظر إلى فضاء متجهي معياري.
انظر أيضا
[عدل]مراجع
[عدل]- ^ أحمد شفيق الخطيب (2001). قاموس العلوم المصور: بالتعريفات والتطبيقات: إنجليزي - عربي (بالعربية والإنجليزية) (ط. 1). بيروت: مكتبة لبنان ناشرون. ص. 184. ISBN:978-9953-10-218-4. OCLC:50131139. QID:Q124741809.
- ^ أحمد شفيق الخطيب (2001). قاموس العلوم المصور: بالتعريفات والتطبيقات: إنجليزي - عربي (بالعربية والإنجليزية) (ط. 1). بيروت: مكتبة لبنان ناشرون. ص. 663. ISBN:978-9953-10-218-4. OCLC:50131139. QID:Q124741809.
- ^ Seymour.، Lipschutz, (2009). Linear algebra (ط. 4th ed). New York: McGraw-Hill. ISBN:9780071543521. OCLC:192082884. مؤرشف من الأصل في 2010-01-12.
{{استشهاد بكتاب}}:|طبعة=يحتوي على نص زائد (مساعدة)صيانة الاستشهاد: أسماء متعددة: قائمة المؤلفين (link) صيانة الاستشهاد: علامات ترقيم زائدة (link)
وصلات خارجية
[عدل]في كومنز صور وملفات عن Scalar product.






















