متعددات الحدود لتشيبيشيف

في الرياضيات، حدوديات تشيبيشيف (بالإنجليزية: Chebyshev polynomials)‏ هي حدوديات يعود اسمها إلى عالم الرياضيات الروسي بافنوتي تشيبيشيف, هي متتالية من حدوديات متعامدة لها صلة بصيغة دي موافر وتعرف ببساطة بواسطة ذاتية الاستدعاء.

عادة هناك فرق بين حدوديات تشيبيشيف من النوع الأول والتي يرمز لها ب T_n وبين حدوديات تشيبيشيف من النوع الثاني ويرمز لها U_n.

حدوديات تشيبيشيف T_n أو U_n هي حدوديات من الدرجة n ومتواليات كثيرات حدود شيبيشيف لأي من النوعين تكون متواليات كثيرات حدود.

حدوديات تشيبيشيف مهمة في نظرية التقريب لأن جذور كثيرات حدود شيبيشيف ذات النوع الأول، والتي يطلق عليها أيضاً عقد شيبيشيف، تستخدم عقدا في استيفاء كثيرات الحدود.

في مجال المعادلات التفاضلية، تأتي حدوديات تشيبيشيف حلولاً لمعادلة تشيبيشيف.

$(1-x^{2})\,y''-x\,y'+n^{2}\,y=0\,\!$

و

$(1-x^{2})\,y''-3x\,y'+n(n+2)\,y=0\,\!$

(الصنف الأول حل للمعادلة الأولى والثاني حل للمعادلة الثانية). هاتان المعادلتان حالتان خاصتان من معادلة ستورم-ليوفيل التفاضلية.

تعريف

تعرف كثيرات حدود شيبيشيف من النوع الأول بالعلاقة التكرارية

${\begin{aligned}T_{0}(x)&=1\\T_{1}(x)&=x\\T_{n+1}(x)&=2xT_{n}(x)-T_{n-1}(x).\end{aligned}}$

وتكون الدالة المولدة التقليدية لـ T_n

$\sum _{n=0}^{\infty }T_{n}(x)t^{n}={\frac {1-tx}{1-2tx+t^{2}}}.\,\!$

ودالة التوليد الأسية هي

$\sum _{n=0}^{\infty }T_{n}(x){\frac {t^{n}}{n!}}={1 \over 2}\left(e^{(x-{\sqrt {x^{2}-1}})t}+e^{(x+{\sqrt {x^{2}-1}})t}\right).\,\!$

تعرف كثيرات حدود شيبيشيف من النوع الثاني بطريقة مشابهة

${\begin{aligned}U_{0}(x)&=1\\U_{1}(x)&=2x\\U_{n+1}(x)&=2xU_{n}(x)-U_{n-1}(x).\end{aligned}}$

من أمثلة الدوال المولدة لـ U_n

$\sum _{n=0}^{\infty }U_{n}(x)t^{n}={\frac {1}{1-2tx+t^{2}}}.\,\!$

تعريف بالنسب المثلثية

النوع الأول:

$T_{n}(x)=\cos(n\arccos x)=\cosh(n\,\mathrm {arccosh} \,x)\,\!$

حيث:

$T_{n}(\cos(\vartheta ))=\cos(n\vartheta )\,\!$

لقيم n = 0, 1, 2, 3,..., أما النوع الثاني:

$U_{n}(\cos(\vartheta ))={\frac {\sin((n+1)\vartheta )}{\sin \vartheta }}\,\!$

لهذه المتطابقة فائدة قصوى مع وجود صيغة التوليد التكرارية لأنها تسمح بحساب جيب التمام لأي تكامل من مضاعفات زاوية بدلالة جيب تمام الزاوية الأساسية.بتقييم كثيرتي حدود شيبيشف الأوليتين:

$T_{0}(x)=\cos \ 0x\ =1\,\!$

و:

$T_{1}(\cos(x))=\cos(x)\,\!$

يمكن بيان أن:

$\cos(2\vartheta )=2\cos \vartheta \cos \vartheta -\cos(0\vartheta )=2\cos ^{2}\,\vartheta -1\,\!$

$\cos(3\vartheta )=2\cos \vartheta \cos(2\vartheta )-\cos \vartheta =4\cos ^{3}\,\vartheta -3\cos \vartheta \,\!$

وهكذا.

تعريف معادلة بل

يمكن تعريف كثيرات حدود شيبيشف أيضاً بأنها حلول معادلة بل

$T_{i}^{2}-(x^{2}-1)U_{i-1}^{2}=1\,\!$

في حلقة R[x]. بالتالي، يمكن توليدها بالطريقة القياسية لمعادلات بل بأخذ قوى حل أساسي:

$T_{i}+U_{i-1}{\sqrt {x^{2}-1}}=(x+{\sqrt {x^{2}-1}})^{i}.\,\!$

العلاقة بين كثيرات حدود شيبيشيف من النوع الأول والنوع الثاني

العلاقة متشابهة بين كثيرات حدود شيبيشيف من النوع الأول والنوع الثاني بالمعالات التالية

${\tfrac {d}{dx}}\,T_{n}(x)=nU_{n-1}(x){\mbox{ , }}n=1,\ldots$

$T_{n}(x)={\frac {1}{2}}(U_{n}(x)-\,U_{n-2}(x)).$

$T_{n+1}(x)=xT_{n}(x)-(1-x^{2})U_{n-1}(x)\,$

$T_{n}(x)=U_{n}(x)-x\,U_{n-1}(x).$

العلاقة التكرارية لمشتقات كثيرات حدود شيبيشيف يمكن اشتقاقها من هذه العلاقات

$2T_{n}(x)={\frac {1}{n+1}}\;{\frac {d}{dx}}T_{n+1}(x)-{\frac {1}{n-1}}\;{\frac {d}{dx}}T_{n-1}(x){\mbox{ , }}\quad n=1,\ldots$

تستعمل هذه العلاقة في طريقة طيفية شيبيشيف لحل المعادلات التفاضلية.

بالمثل، يمكن تعريف التعاقبين من أزواج معادلات تكرار متبادل:

$T_{0}(x)=1\,\!$

$U_{-1}(x)=0\,\!$

$T_{n+1}(x)=xT_{n}(x)-(1-x^{2})U_{n-1}(x)\,$

$U_{n}(x)=xU_{n-1}(x)+T_{n}(x)\,$

صيغ صريحة

$T_{n}(x)={\begin{cases}\cos(n\arccos(x)),&\ x\in [-1,1]\\\cosh(n\,\mathrm {arccosh} (x)),&\ x\geq 1\\(-1)^{n}\cosh(n\,\mathrm {arccosh} (-x)),&\ x\leq -1\\\end{cases}}\,\!$

${\begin{aligned}T_{n}(x)&={\frac {(x-{\sqrt {x^{2}-1}})^{n}+(x+{\sqrt {x^{2}-1}})^{n}}{2}}\\&=\sum _{k=0}^{\lfloor n/2\rfloor }{\binom {n}{2k}}(x^{2}-1)^{k}x^{n-2k}\\&=x^{n}\sum _{k=0}^{\lfloor n/2\rfloor }{\binom {n}{2k}}(1-x^{-2})^{k}\\&={\frac {n}{2}}\sum _{k=0}^{\lfloor n/2\rfloor }(-1)^{k}{\frac {(n-k-1)!}{k!(n-2k)!}}~(2x)^{n-2k}\quad (n>0)\\&=n\sum _{k=0}^{n}(-2)^{k}{\frac {(n+k-1)!}{(n-k)!(2k)!}}(1-x)^{k}\quad (n>0)\\&=\,_{2}F_{1}\left(-n,n;{\frac {1}{2}};{\frac {1-x}{2}}\right)\\\end{aligned}}$

${\begin{aligned}U_{n}(x)&={\frac {(x+{\sqrt {x^{2}-1}})^{n+1}-(x-{\sqrt {x^{2}-1}})^{n+1}}{2{\sqrt {x^{2}-1}}}}\\&=\sum _{k=0}^{\lfloor n/2\rfloor }{\binom {n+1}{2k+1}}(x^{2}-1)^{k}x^{n-2k}\\&=x^{n}\sum _{k=0}^{\lfloor n/2\rfloor }{\binom {n+1}{2k+1}}(1-x^{-2})^{k}\\&=\sum _{k=0}^{\lfloor n/2\rfloor }{\binom {2k-(n+1)}{k}}~(2x)^{n-2k}\quad (n>0)\\&=\sum _{k=0}^{\lfloor n/2\rfloor }(-1)^{k}{\binom {n-k}{k}}~(2x)^{n-2k}\quad (n>0)\\&=\sum _{k=0}^{n}(-2)^{k}{\frac {(n+k+1)!}{(n-k)!(2k+1)!}}(1-x)^{k}\quad (n>0)\\&=(n+1)\,_{2}F_{1}\left(-n,n+2;{\frac {3}{2}};{\frac {1-x}{2}}\right)\end{aligned}}$

حيث $_{2}F_{1}$ هي دالة مثلثية زائدية.

الخواص

التحويل

من المتطابقات المفيدة في تحويل كثيرات الحدود

$T_{n}\left(1-2x^{2}\right)=(-1)^{n}T_{2n}(x)$

و

$U_{n}\left(1-2x^{2}\right)x=(-1)^{n}U_{2n+1}(x).$

الجذور والقيم القصوى

لأي من النوعين في كثيرات حدود شيبيشف من الدرجة n يوجد لها n جذور بسيطة مختلفة تدعى جذور شيبيشف في الفترة [−1,1]. باستعمال التعريف المثلثي والحقيقة القائلة بأن

$\cos \left({\frac {\pi }{2}}\,(2k+1)\right)=0$

يمن إثبات أن جذور T_n هي

$x_{k}=\cos \left({\frac {\pi }{2}}\,{\frac {2k-1}{n}}\right),\quad k=1,\ldots ,n.$

بالمثل جذور U_n هي

$x_{k}=\cos \left({\frac {k}{n+1}}\pi \right),\quad k=1,\ldots ,n.$

التفاضل والتكامل

باشتقاق كثيرات الحدود في صورها المثلثية، يمكن بسهولة الوصل لايلي:

${\frac {dT_{n}}{dx}}=nU_{n-1}\,$

${\frac {dU_{n}}{dx}}={\frac {(n+1)T_{n+1}-xU_{n}}{x^{2}-1}}\,$

${\frac {d^{2}T_{n}}{dx^{2}}}=n{\frac {nT_{n}-xU_{n-1}}{x^{2}-1}}=n{\frac {(n+1)T_{n}-U_{n}}{x^{2}-1}}.\,$

التعامدية

إن كلا من T_n وU_n تكونان متواليات كثيرات حدود متعامدة. كثيرات الحدود من النوع الأول تكون متعامدة بالنسبة للوزن

${\frac {1}{\sqrt {1-x^{2}}}},\,\!$

في الفترة (−1,1), أي أن:

$\int _{-1}^{1}T_{n}(x)T_{m}(x)\,{\frac {dx}{\sqrt {1-x^{2}}}}={\begin{cases}0&:n\neq m\\\pi &:n=m=0\\\pi /2&:n=m\neq 0\end{cases}}$

بالمثل، كثيرات الحدود من النوع الثاني تكون متعامدة بالنسبة للوزن

${\sqrt {1-x^{2}}}\,\!$

على الفترة [−1,1], أي أن:

$\int _{-1}^{1}U_{n}(x)U_{m}(x){\sqrt {1-x^{2}}}\,dx={\begin{cases}0&:n\neq m,\\\pi /2&:n=m.\end{cases}}$

الأصغرية ∞-طبيعي

لأي قيمة n ≥ 1, بين كثيرات الحدود من الدرجة nمع معامل أسبقية 1,

$f(x)={\frac {1}{2^{n-1}}}T_{n}(x)$

هي تلك التي لها قيمة مطلقة أعظمية في الفترة [−1, 1] تكون أصغرية.

هذه القيمة الأعظمية تكون

${\frac {1}{2^{n-1}}}$

و|ƒ(x)| تصل لهذه القيمة العظمى تماماً n + 1 من المرات: عند

$x=\cos {\frac {k\pi }{n}}{\text{ for }}0\leq k\leq n.$

صلتها بكثيرات حدود أخرى

• $T_{n}(x)={\frac {1}{n-{\frac {1}{2}} \choose n}}P_{n}^{-{\frac {1}{2}},-{\frac {1}{2}}}(x)={\frac {n}{2}}C_{n}^{0}(x),$
• $U_{n}(x)={\frac {1}{2{n+{\frac {1}{2}} \choose n}}}P_{n}^{{\frac {1}{2}},{\frac {1}{2}}}(x)=C_{n}^{1}(x).$

أمثلة

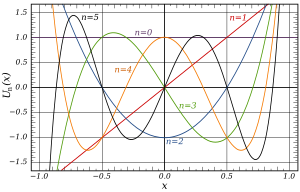
بعض من كثيرات حدود شيبيشف الأولى من النوع الأول في المجال −1 < x < 1: الأسطح T₀, T₁, T₂, T₃, T₄ وT₅.

بعض كثيرات حدود شيبيشف الأولى من النوع الأول هي

$T_{0}(x)=1\,$

$T_{1}(x)=x\,$

$T_{2}(x)=2x^{2}-1\,$

$T_{3}(x)=4x^{3}-3x\,$

$T_{4}(x)=8x^{4}-8x^{2}+1\,$

$T_{5}(x)=16x^{5}-20x^{3}+5x\,$

$T_{6}(x)=32x^{6}-48x^{4}+18x^{2}-1\,$

$T_{7}(x)=64x^{7}-112x^{5}+56x^{3}-7x\,$

$T_{8}(x)=128x^{8}-256x^{6}+160x^{4}-32x^{2}+1\,$

خطأ رياضيات (خطأ في الصياغة): {\displaystyle T_9(x) = 256x^9 – 576x^7 + 432x^5 – 120x^3 + 9x. \,}

بعض من كثيرات حدود شيبيشف الأولى من النوع الثاني في المجال −1 < x < 1: الأسطح U₀, U₁, U₂, U₃, U₄ وU₅.

بعض كثيرات حدود شيبيشف الأولى من النوع الثاني هي

$U_{0}(x)=1\,$

$U_{1}(x)=2x\,$

$U_{2}(x)=4x^{2}-1\,$

$U_{3}(x)=8x^{3}-4x\,$

$U_{4}(x)=16x^{4}-12x^{2}+1\,$

$U_{5}(x)=32x^{5}-32x^{3}+6x\,$

$U_{6}(x)=64x^{6}-80x^{4}+24x^{2}-1\,$

$U_{7}(x)=128x^{7}-192x^{5}+80x^{3}-8x\,$

$U_{8}(x)=256x^{8}-448x^{6}+240x^{4}-40x^{2}+1\,$

$U_{9}(x)=512x^{9}-1024x^{7}+672x^{5}-160x^{3}+10x.\,$

كمجموعة أساسات

في فضاء سوبوليف, تؤلف مجموعة كثيرات حدود شيبيشف مجموعة أساس مكتملة بحيث أن دالة في نفس الفضاء يمكن التعبير عنها على −1 ≤ x ≤ 1 بالنشر:

$f(x)=\sum _{n=0}^{\infty }a_{n}T_{n}(x).$

مثال 1

ليكن لدينا منشور شيبيشيف $\log(1+x)$. يمكن التعبير عنه

$\log(1+x)=\sum _{n=0}^{\infty }a_{n}T_{n}(x).$

كما يمكن إيجاد المعاملات $a_{n}$ إما بتطبيق الضرب الداخلي أو من شرط التعامدية المتقطعة. بطريقة الضرب الداخلي

$\int _{-1}^{+1}{\frac {T_{m}(x)\log(1+x)}{\sqrt {1-x^{2}}}}dx=\sum _{n=0}^{\infty }a_{n}\int _{-1}^{+1}{\frac {T_{m}(x)T_{n}(x)}{\sqrt {1-x^{2}}}}dx,$

نحصل على

$a_{n}={\begin{cases}-\log(2)&:n=0\\{\frac {-2(-1)^{n}}{n}}&:n>0.\end{cases}}$

بالمثل وعند عدم جدوى طريقة الضرب الداخلي نلجأ لطريقة شرط التعامدية المتقطعة فنحصل على

$a_{n}={\frac {2-\delta _{0n}}{N}}\sum _{k=0}^{N-1}T_{n}(x_{k})\log(1+x_{k}),$

حيث $\delta _{ij}$ هي دالة دلتا كرونكر و$x_{k}$ هي N أصفار $T_{N}(x)$ من غاوس–لوباتو

$x_{k}=\cos \left({\frac {\pi \left(k+{\frac {1}{2}}\right)}{N}}\right).$

وبحساب المعاملات $a_{n}$ بواسطة تحويل جيب التمام المتقطع

$a_{n}={\frac {2-\delta _{0n}}{N}}\sum _{k=0}^{N-1}\cos \left({\frac {n\pi \left(k+{\frac {1}{2}}\right)}{N}}\right)\log(1+x_{k}).$

مثال 2

${\begin{aligned}(1-x^{2})^{\alpha }=&-{\frac {1}{\sqrt {\pi }}}{\frac {\Gamma ({\frac {1}{2}}+\alpha )}{\Gamma (\alpha +1)}}+2^{1-2\alpha }\sum _{n=0}(-1)^{n}{2\alpha \choose \alpha -n}T_{2n}(x)\\=&2^{-2\alpha }\sum _{n=0}(-1)^{n}{2\alpha +1 \choose \alpha -n}U_{2n}(x).\end{aligned}}$

انظر أيضا

• متعددات الحدود لهيرمت
• نظرية التقريب
• تباين الأخوين ماركوف