مجسم أرخميدي

في الهندسة الرياضية، مجسم أرخميدي هو واحد من 13 مجسم عدّدها أرخميدس لأول مرة. إنها متعددة السطوح المنتظمة المحدبة المكونة من مضلعات منتظمة تلتقي في رؤوس متطابقة، باستثناء المجسمات الأفلاطونية الخمسة (التي تتكون من نوع واحد فقط من المضلعات) باستثناء المنشورات والمنشورات المضادة. وهي تختلف عن مجسمات جونسون التي لا تلتقي وجوهها التي هي عبارة عن مضلعات منتظمة في رؤوس متطابقة.
أصل التسمية
[عدل]تأخذ اسمها من أرخميدس، الذي ناقش العمل خلال نهضة الرياضيات والتوصل إلى هذه القيم من أشكال نقية واكتشاف كل من هذه الأشكال.
اكتمل هذا البحث حول 1620 من قبل يوهانس كبلر، [1] الذي يعرف المناشير، منشور مضاد، والمواد الصلبة غير محدب والمعروفة باسم متعددات السطوح كبلر-بوانسو [الإنجليزية]
التصنيف
[عدل]هناك 13 أرخميدس المواد الصلبة (15 إذا كان مرآة صورة ق اثنين من enantiomorphs، انظر أدناه، تحسب على حدة).
هنا في تكوين قمة الرأس يشير إلى نوع من المضلعات المنتظمة التي تحقق في أي قمة معين. على سبيل المثال، قمة التكوين من (4,6,8) يعني أن مربع، مسدس، ومثمن نلتقي في قمة الرأس (مع أن في اتجاه عقارب الساعة من أجل المتخذة حول قمة الرأس).
| الاسم (Vertex configuration) |
شفّاف | الصلب | شبكة | الوجوه | الزوايا | Vertices | مجموعة النقاط | |
|---|---|---|---|---|---|---|---|---|
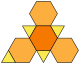
| truncated tetrahedron (3.6.6) |
 (Animation) |

|
|
8 | 4 triangles 4 سداسي أضلاعs |
18 | 12 | Td |
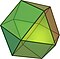
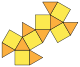
| مقطوع المكعب الثماني (3.4.3.4) |
 (Animation) |

|
|
14 | 8 مثلثs 6 مربع |
24 | 12 | Oh |
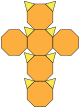
| مكعب مقطع الرؤوس أو سداسي الأوجه مقطع الرؤوس (3.8.8) |
 (Animation) |

|
|
14 | 8 triangles 6 مثمنs |
36 | 24 | Oh |
| truncated octahedron (4.6.6) |
 |

|

|
14 | 6 squares 8 hexagons |
36 | 24 | Oh |
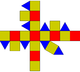
| rhombicuboctahedron or small rhombicuboctahedron (3.4.4.4 ) |
 (Animation) |

|
|
26 | 8 triangles 18 squares |
48 | 24 | Oh |
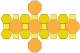
| truncated cuboctahedron or great rhombicuboctahedron (4.6.8) |
 (Animation) |

|
|
26 | 12 squares 8 hexagons 6 octagons |
72 | 48 | Oh |
| snub cube or snub hexahedron or snub cuboctahedron (2 لا انطباقية forms) (3.3.3.3.4) |
 (Animation)  (Animation) |

|

|
38 | 32 triangles 6 squares |
60 | 24 | O |
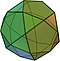
| icosidodecahedron (3.5.3.5) |
 (Animation) |

|

|
32 | 20 triangles 12 خماسي أضلاعs |
60 | 30 | Ih |
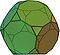
| truncated dodecahedron (3.10.10) |
 (Animation) |

|

|
32 | 20 triangles 12 عشاري أضلاعs |
90 | 60 | Ih |
| عشروني أوجه مقطع الرؤوس (5.6.6 ) |
 (Animation) |

|

|
32 | 12 pentagons 20 hexagons |
90 | 60 | Ih |
| rhombicosidodecahedron or small rhombicosidodecahedron (3.4.5.4) |
 (Animation) |

|

|
62 | 20 triangles 30 squares 12 pentagons |
120 | 60 | Ih |
| truncated icosidodecahedron or great rhombicosidodecahedron (4.6.10) |
 (Animation) |

|

|
62 | 30 squares 20 hexagons 12 decagons |
180 | 120 | Ih |
| snub dodecahedron or snub icosidodecahedron (2 لا انطباقية forms) (3.3.3.3.5) |
 (Animation)  (Animation) |

|

|
92 | 80 triangles 12 pentagons |
150 | 60 | I |
بعض التعاريف من semiregular polyhedron تشمل واحدة أكثر شخصية، ، the elongated square gyrobicupola or "pseudo-rhombicuboctahedron".[2]
خصائص
[عدل]عدد الرؤوس هو 720 درجة مقسومة على قمة الرأس . وهذه هي المواد الصلبة وجها موحدا مع القمم العادية.
انظر أيضا
[عدل]- تبليط لادوري
- مجسم أفلاطوني
- شبه بلورة
- semiregular polyhedron
- متعدد سطوح منتظم
- uniform polyhedron
- حول توازن السطوح
الملاحظات
[عدل]- ^ Field J., Rediscovering the Archimedean Polyhedra: Piero della Francesca, Luca Pacioli, Leonardo da Vinci, Albrecht Dürer, Daniele Barbaro, and Johannes Kepler, Archive for History of Exact Sciences, 50, 1997, 227
- ^ Malkevitch (1988), p. 85
المراجع
[عدل]- Jayatilake، Udaya (مارس 2005). "Calculations on face and vertex regular polyhedra". Mathematical Gazette. ج. 89 ع. 514: 76–81.
- قالب:The Geometrical Foundation of Natural Structure (book) (Section 3-9)
- Malkevitch، Joseph (1988)، "Milestones in the history of polyhedra"، في Senechal، M.؛ Fleck، G. (المحررون)، Shaping Space: A Polyhedral Approach، Boston: Birkhäuser، ص. 80–92.
وصلات خارجية
[عدل]- إيريك ويستاين، Archimedean solid، ماثوورلد Mathworld (باللغة الإنكليزية).
- Archemedian Solids by إيريك ويستاين، Wolfram Demonstrations Project.
- Paper models of Archimedean Solids and Catalan Solids
- Free paper models(nets) of Archimedean solids
- The Uniform Polyhedra by Dr. R. Mäder
- Virtual Reality Polyhedra, The Encyclopedia of Polyhedra by George W. Hart
- Penultimate Modular Origami by James S. Plank
- Interactive 3D polyhedra in Java
- Stella: Polyhedron Navigator: Software used to create many of the images on this page.
- Paper Models of Archimedean (and other) Polyhedra

