مستخدم:Dina El Shobaky/ملعب10
| جزء من سلسلة مقالات حول |
| التفاضل والتكامل |
|---|
| بوابة رياضيات |
في تفاضل شعاعى والهندسة التفاضلية بشكل عام نظرية ستوكس (تسمى أيضا نظرية ستوكس المعممة أو نظرية ستوكس-كارتان) [1]، التي صيغت من قبل إيلي كارتن [2]في أعقاب العمل السابق على تعميم نظريات حساب المتجه من قبل فيتو فولتيرا، إدوارد جورسات وهنري بوانكاريه [3][4] هو بيان عن تكامل الأشكال التفاضلية على متعدد شعب، والتي تبسط وتعمم العديد مبرهنة من التفاضل الاتجاهى . نظرية ستوكس تقول أن التكامل من شكل تفاضلي ω على متعدد شعب مستطيلة Ω يساوي تكامل مشتق خارجي لها dω على كامل Ω,
هذا الشكل الحديث من نظرية ستوكس هو تعميم واسع من نتيجة الكلاسيكية. أرسل اللورد كلفن إلى جورج ستوكس في رسالة مؤرخة في 2 يوليو 1850. [5][6][7] وضع ستوكس النظرية كمسألة في امتحان جائزة سميث 1854، مما أدى إلى نتيجة تحمل اسمه، على الرغم من أنه كان أول من نشر هيرمان هانكيل في عام 1861. [7] [8]هذه النظرية الكلاسيكية كلفن-ستوكس تتصل التكامل السطحية للضفيرة من حقل ناقلات F على سطح Σ في الإقليدية ثلاثة الفضاء إلى التكامل خط من حقل ناقلات عبر حدودها Σ∂:
هذا البيان الكلاسيكي، جنبا إلى جنب مع نظرية الاختلاف الكلاسيكي، والنظرية الأساسية لحساب التفاضل والتكامل، ونظرية غرين هي ببساطة حالات خاصة من الصيغة العامة المذكورة أعلاه.
Introduction
[عدل]المبرهنة الأساسية للتفاضل والتكامل تنص على أنه يمكن حساب تكامل الدالة f على الفاصل الزمني [a، b] من خلال إيجاد مشتق عكسي F من f :
نظرية ستوكس هي تعميم واسع لهذه النظرية بالمعنى التالي:
- من خلال اختيار (F, df/dx =f(x في صيغة الأشكال التفاضلية، وهذا يقول أن f(x) dx هو مشتق خارجي من 0-فورم، أي وظيفه F, وبعبارة أخرى dF = f dx . تنطبق نظرية ستوكس العامة على أشكال تفاضلية أعلى ω بدلا من 0-فورم مثل F.
- الفاصل الزمني المغلق [a، b] هو مثال بسيط على متعدد شعب أحادي البعد . حدودها هي مجموعة تتكون من نقطتين a,b . ويمكن تعميم التكامل f عبر الفاصل الزمني على دمج الأشكال على مشعب أعلى الأبعاد. هناك حاجة إلى اثنين من الشروط التقنية: يجب أن تكون متعددة مشعب، والشكل يجب أن تكون معتمدة على دعم (رياضيات) من أجل إعطاء متكاملة بشكل جيد.
- النقطتان a و b تشكل حدود الفاصل الزمني المغلق. وبصورة أعم، تنطبق نظرية ستوكس على الفتحات الموجهة M مع الحدود. الحدود M∂ من M هو في حد ذاته مشعب ويرث دوران طبيعي من أن M. على سبيل المثال، الدوران الطبيعي للفاصل يعطي توجها للنقطتين محددتين . بشكل حدسي، يرث الاتجاه المعاكس b، كما هي في طرفي نقيض من الفاصل الزمني. لذلك، "دمج" F على نقطتين الحدود a، b أخذ الفرق F(b) − F(a).
وبعبارات أبسط من ذلك، يمكن للمرء أن يعتبر أن النقاط يمكن اعتبارها حدود المنحنيات، التي هي حدود 0 الأبعاد الأبعاد متعددة الفتحات. لذلك، كما يمكن للمرء أن يجد قيمة لا يتجزأ f dx = dF على مشعب 1-الأبعاد {a, b} من خلال النظر في مشتق المضادة (F) على حدود 0 الأبعاد ({b، a)، يمكن للمرء أن تعميم نظرية أساسية لحساب التفاضل والتكامل، مع عدد قليل من المحاذير إضافية، للتعامل مع قيمة تكاملات (dω) على مشعب ن الأبعاد (Ω) من خلال النظر في أنتيديريفاتيف (ω) في (n − 1) - حدود ديمنزيونال ∂Ω من المنوع.
لذا فإن النظرية الأساسية تقرأ:
Formulation for smooth manifolds with boundary
[عدل]اسمحوا Ω يكون مشعب السلس المنحى مع حدود البعد n والسماح α يكون على شكل ن التفاضلي السلس الذي يتم دعم مضغوط على Ω. أولا، افترض أن α يتم دعمها بشكل مضغوط في مجال مخطط إحداثي واحد موجه {U, φ}. في هذه الحالة، ونحن نحدد تكامل α أكثر من Ω كما
أي عن طريق سحب α إلى Rn
وبصورة أعم، يتم تعريف تكامل α على Ω على النحو التالي: اسمحوا {ψi} أن يكون قسم للوحدة مرتبطا بغطاء محدود محليا {Ui, φi} من (ينسق باستمرار) تنسيق المخططات، ثم حدد التكامل:
حيث يتم تقييم كل مصطلح في المجموع عن طريق سحب إلى Rn كما هو موضح أعلاه. وهذه الكمية محددة جيدا؛ أي أنه لا يعتمد على اختيار المخططات الإحداثيات ولا تقسيم الوحدة.
Conventionally, is abbreviated as , since the pullback of a differential form by the inclusion map is simply its restriction to its domain: . Here is the exterior derivative, which is defined using the manifold structure only. The right-hand side is sometimes written as to stress the fact that the -manifold has no boundary.[note 1] (This fact is also an implication of Stokes' theorem, since for a given smooth -dimensional manifold , application of the theorem twice gives for any -form , which implies that .) The right-hand side of the equation is often used to formulate integral laws; the left-hand side then leads to equivalent differential formulations (see below).
The theorem is often used in situations where is an embedded oriented submanifold of some bigger manifold, often , on which the form is defined.
Topological preliminaries; integration over chains
[عدل]السماح M يكون مشعب على نحو سلس. ويعرف A (السلس) المفرد k- البسيط في M على أنها خريطة سلسة من البسيط القياسية في Rk إلى M. المجموعة Ck(M, Z) من المفرد k- سلاسل على M يعرف أن تكون المجموعة الحرة أبيليان على مجموعة من المفردات k- سيمبليسس في M. هذه المجموعات، جنبا إلى جنب مع خريطة الحدود،∂، تحديد سلسلة معقدة. مجموعة التماثل المقابلة (مجموعة كوهومولوغي) هي إيسومورفيك لمجموعة التماثل المفردة المعتادة Hk(M, Z) مجموعة المفردات كوهومولوغي المفردة Hk(M, Z) والتي تم تعريفها باستخدام سيمبليسس المتواصلة بدلا من السلس في M .
من ناحية أخرى، فإن الأشكال التفاضلية، مع مشتق خارجي، d، كخريطة ربط، تشكل مجمع كوتشين، الذي يحدد مجموعات رهام كوهومولوغيHk
dR(M, R) .
.
يمكن دمج أشكال k التفاضلية عبر k-سيمبلكس بطريقة طبيعية، عن طريق سحب إلى Rk. تمديد بالخطي يسمح واحد لدمج عبر سلاسل. وهذا يعطي خريطة خطية من فضاء k- أشكال إلى مجموعة كث من كوشينز المفرد Ck(M, Z), وظيفية الخطية علىCk(M, Z) . وبعبارة أخرى، يحدد شكل k ω وظيفيا.
on the k-chains. Stokes' theorem says that this is a chain map from de Rham cohomology to singular cohomology with real coefficients; the exterior derivative, d, behaves like the dual of ∂ on forms. This gives a homomorphism from de Rham cohomology to singular cohomology. On the level of forms, this means:
- closed forms, i.e., dω = 0, have zero integral over boundaries, i.e. over manifolds that can be written as ∂∑c Mc, and
- exact forms, i.e., ω = dσ, have zero integral over cycles, i.e. if the boundaries sum up to the empty set: ∑c Mc = ∅.
De Rham's theorem shows that this homomorphism is in fact an isomorphism. So the converse to 1 and 2 above hold true. In other words, if {ci} are cycles generating the kth homology group, then for any corresponding real numbers, {ai}, there exist a closed form, ω, such that
and this form is unique up to exact forms.
Underlying principle
[عدل]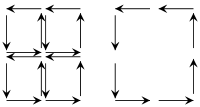
To simplify these topological arguments, it is worthwhile to examine the underlying principle by considering an example for d = 2 dimensions. The essential idea can be understood by the diagram on the left, which shows that, in an oriented tiling of a manifold, the interior paths are traversed in opposite directions; their contributions to the path integral thus cancel each other pairwise. As a consequence, only the contribution from the boundary remains. It thus suffices to prove Stokes' theorem for sufficiently fine tilings (or, equivalently, simplices), which usually is not difficult.
Generalization to rough sets
[عدل]
The formulation above, in which Ω is a smooth manifold with boundary, does not suffice in many applications. For example, if the domain of integration is defined as the plane region between two x-coordinates and the graphs of two functions, it will often happen that the domain has corners. In such a case, the corner points mean that Ω is not a smooth manifold with boundary, and so the statement of Stokes' theorem given above does not apply. Nevertheless, it is possible to check that the conclusion of Stokes' theorem is still true. This is because Ω and its boundary are well-behaved away from a small set of points (a measure zero set).
A version of Stokes' theorem that extends to rough domains was proved by Whitney.[9] Assume that D is a connected bounded open subset of Rn. Call D a standard domain if it satisfies the following property: There exists a subset P of ∂D, open in ∂D, whose complement in ∂D has Hausdorff (n − 1)-measure zero; and such that every point of P has a generalized normal vector. This is a vector v(x) such that, if a coordinate system is chosen so that v(x) is the first basis vector, then, in an open neighborhood around x, there exists a smooth function f(x2, …, xn) such that P is the graph { x1 = f(x2, …, xn) } and D is the region { x1 < f(x2, …, xn) }. Whitney remarks that the boundary of a standard domain is the union of a set of zero Hausdorff (n − 1)-measure and a finite or countable union of smooth (n − 1)-manifolds, each of which has the domain on only one side. He then proves that if D is a standard domain in Rn, ω is an (n − 1)-form which is defined, continuous, and bounded on D ∪ P, smooth on D, integrable on P, and such that dω is integrable on D, then Stokes' theorem holds, that is,
The study of measure-theoretic properties of rough sets leads to geometric measure theory. Even more general versions of Stokes' theorem have been proved by Federer and by Harrison.[10]
Special cases
[عدل]The general form of the Stokes theorem using differential forms is more powerful and easier to use than the special cases. The traditional versions can be formulated using Cartesian coordinates without the machinery of differential geometry, and thus are more accessible. Further, they are older and their names are more familiar as a result. The traditional forms are often considered more convenient by practicing scientists and engineers but the non-naturalness of the traditional formulation becomes apparent when using other coordinate systems, even familiar ones like spherical or cylindrical coordinates. There is potential for confusion in the way names are applied, and the use of dual formulations.
Kelvin–Stokes theorem
[عدل]
This is a (dualized) 1 + 1-dimensional case, for a 1-form (dualized because it is a statement about vector fields). This special case is often just referred to as Stokes' theorem in many introductory university vector calculus courses and as used in physics and engineering. It is also sometimes known as the curl theorem.
The classical Kelvin–Stokes theorem:
which relates the surface integral of the curl of a vector field over a surface Σ in Euclidean three-space to the line integral of the vector field over its boundary, is a special case of the general Stokes theorem (with n = 2) once we identify a vector field with a 1-form using the metric on Euclidean 3-space. The curve of the line integral, ∂Σ, must have positive orientation, meaning that dr points counterclockwise when the surface normal, dΣ, points toward the viewer, following the right-hand rule.
One consequence of the Kelvin–Stokes theorem is that the field lines of a vector field with zero curl cannot be closed contours. The formula can be rewritten as:
where P, Q and R are the components of F.
These variants are rarely used:
Green's theorem
[عدل]Green's theorem is immediately recognizable as the third integrand of both sides in the integral in terms of P, Q, and R cited above.
In electromagnetism
[عدل]Two of the four Maxwell equations involve curls of 3-D vector fields and their differential and integral forms are related by the Kelvin–Stokes theorem. Caution must be taken to avoid cases with moving boundaries: the partial time derivatives are intended to exclude such cases. If moving boundaries are included, interchange of integration and differentiation introduces terms related to boundary motion not included in the results below (see Differentiation under the integral sign):
| Name | Differential form | Integral form (using Kelvin–Stokes theorem plus relativistic invariance, ∫ ∂∂t … → ddt ∫ …) |
|---|---|---|
| Maxwell–Faraday equation |
(with C and S not necessarily stationary) | |
| Ampère's law (with Maxwell's extension): |
(with C and S not necessarily stationary) |
The above listed subset of Maxwell's equations are valid for electromagnetic fields expressed in SI units. In other systems of units, such as CGS or Gaussian units, the scaling factors for the terms differ. For example, in Gaussian units, Faraday's law of induction and Ampère's law take the forms:[11][12]
respectively, where c is the speed of light in vacuum.
Divergence theorem
[عدل]Likewise, the Ostrogradsky–Gauss theorem (also known as the divergence theorem or Gauss's theorem)
is a special case if we identify a vector field with the (n − 1)-form obtained by contracting the vector field with the Euclidean volume form. An application of this is the case F = fc where c is an arbitrary constant vector. Working out the divergence of the product gives
Since this holds for all c we find
Footnotes
[عدل]- ^ For mathematicians this fact is known, therefore the circle is redundant and often omitted. However, one should keep in mind here that in thermodynamics, where frequently expressions as ∮W {dtotalU} appear (wherein the total derivative, see below, should not be confused with the exterior one), the integration path W is a one-dimensional closed line on a much higher-dimensional manifold. That is, in a thermodynamic application, where U is a function of the temperature α1 := T, the volume α2 := V, and the electrical polarization α3 := P of the sample, one has
References
[عدل]- ^ Physics of Collisional Plasmas - Introduction to | Michel Moisan | Springer (بالإنجليزية).
- ^ Cartan، Élie (1945). Les Systèmes Différentiels Extérieurs et leurs Applications Géométriques. Paris: Hermann.
- ^ Katz، Victor J. (1 يناير 1979). "The History of Stokes' Theorem". Mathematics Magazine. ج. 52 ع. 3: 146–156. DOI:10.2307/2690275. JSTOR:2690275.
- ^ Katz، Victor J. (1999). "5. Differential Forms". في James، I. M. (المحرر). History of Topology. Amsterdam: Elsevier. ص. 111–122. ISBN:9780444823755.
- ^ See:
- [1]
- The letter from Thomson to Stokes appears in: Thomson، William؛ Stokes، George Gabriel (1990). Wilson، David B. (المحرر). The Correspondence between Sir George Gabriel Stokes and Sir William Thomson, Baron Kelvin of Largs, Volume 1: 1846–1869. Cambridge, England: Cambridge University Press. ص. 96–97.
- Neither Thomson nor Stokes published a proof of the theorem. The first published proof appeared in 1861 in: Hankel، Hermann (1861). Zur allgemeinen Theorie der Bewegung der Flüssigkeiten [On the general theory of the movement of fluids]. Göttingen, Germany: Dieterische University Buchdruckerei. ص. 34–37. Hankel doesn't mention the author of the theorem.
- In a footnote, Larmor mentions earlier researchers who had integrated, over a surface, the curl of a vector field. See: Stokes، George Gabriel (1905). Larmor، Joseph؛ Strutt، John William, Baron Rayleigh (المحررون). Mathematical and Physical Papers by the late Sir George Gabriel Stokes. Cambridge, England: University of Cambridge Press. ج. 5. ص. 320–321.
{{استشهاد بكتاب}}: صيانة الاستشهاد: أسماء متعددة: قائمة المحررين (link)
- ^ Darrigol، Olivier (2000). Electrodynamics from Ampère to Einstein. Oxford, England. ص. 146. ISBN:0198505930.
{{استشهاد بكتاب}}: صيانة الاستشهاد: مكان بدون ناشر (link) - ^ ا ب Spivak (1965), p. vii, Preface.
- ^ See:
- The 1854 Smith's Prize Examination is available online at: Clerk Maxwell Foundation. Maxwell took this examination and tied for first place with Edward John Routh. See: Clerk Maxwell، James (1990). Harman، P. M. (المحرر). The Scientific Letters and Papers of James Clerk Maxwell, Volume I: 1846–1862. Cambridge, England: Cambridge University Press. ص. 237, footnote 2. See also Smith's prize or the Clerk Maxwell Foundation.
- Clerk Maxwell، James (1873). A Treatise on Electricity and Magnetism. Oxford, England: Clarendon Press. ج. 1. ص. 25–27. In a footnote on page 27, Maxwell mentions that Stokes used the theorem as question 8 in the Smith's Prize Examination of 1854. This footnote appears to have been the cause of the theorem's being known as "Stokes' theorem".
- ^ Whitney, Geometric Integration Theory, III.14.
- ^ Harrison، J. (أكتوبر 1993). "Stokes' theorem for nonsmooth chains". Bulletin of the American Mathematical Society (New Series). ج. 29 ع. 2.
- ^ Jackson، J. D. (1975). Classical Electrodynamics (ط. 2nd). New York, NY: Wiley.
- ^ Born، M.؛ Wolf، E. (1980). Principles of Optics (ط. 6th). Cambridge, England: Cambridge University Press.
Further reading
[عدل]- Joos، Georg (1980). Theoretische Physik (ط. 13th). Wiesbaden, Germany: Akademische Verlagsgesellschaft. ISBN:3-400-00013-2.
- Katz، Victor J. (مايو 1979). "The History of Stokes' Theorem". Mathematics Magazine. ج. 52 ع. 3: 146–156. DOI:10.2307/2690275. JSTOR:2690275.
- Marsden، Jerrold E.؛ Anthony، Tromba (2003). Vector Calculus (ط. 5th). W. H. Freeman.
- Lee، John (2003). Introduction to Smooth Manifolds. Springer-Verlag. ISBN:978-0-387-95448-6.
- Rudin، Walter (1976). Principles of Mathematical Analysis (PDF). New York, NY: McGraw–Hill. ISBN:0-07-054235-X.
- Spivak، Michael (1965). Calculus on Manifolds: A Modern Approach to Classical Theorems of Advanced Calculus (PDF). New York: W. A. Benjamin, Inc. ISBN:978-0-8053-9021-6. (See Calculus on Manifolds)
- Madsen، Ib؛ Tornehave، Jørgen (1997). From Calculus to Cohomology: De Rham cohomology and characteristic classes (PDF). Cambridge, UK: Cambridge University Press. ISBN:0-521-58956-8.
- Loomis، Lynn Harold؛ Sternberg، Shlomo (2014). Advanced Calculus (PDF). Hackensack, New Jersey: World Scientific. ISBN:978-981-4583-93-0.
- Tu، Loring W. (2011). An Introduction to Manifolds (PDF) (ط. 2nd). New York: Springer. ISBN:978-1-4419-7399-3.
- Stewart، James (2001). Calculus: Concepts and Contexts (ط. 2nd). Pacific Grove, CA: Brooks/Cole.
- Stewart، James (2003). Calculus: Early Transcendental Functions (ط. 5th). Brooks/Cole.
External links
[عدل]- Hazewinkel, Michiel, ed. (2001), "Stokes formula", Encyclopedia of Mathematics (بالإنجليزية), Springer, ISBN:978-1-55608-010-4
- Proof of the Divergence Theorem and Stokes' Theorem
- Calculus 3 – Stokes Theorem from lamar.edu – an expository explanation
تصنيف:Differential topology
تصنيف:Differential forms
تصنيف:Duality theories
تصنيف:Integration on manifolds
تصنيف:Theorems in calculus
تصنيف:Theorems in differential geometry




![{\displaystyle \int _{[a,b]}f(x)\,dx=\int _{[a,b]}dF=\int _{\{a\}^{-}\cup \{b\}^{+}}F=F(b)-F(a)\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23cc3c08d9bb869053461d0eb1e277cc309f09c9)




















![{\displaystyle {\begin{aligned}\iint _{\Sigma }&{\Bigg (}\left({\frac {\partial R}{\partial y}}-{\frac {\partial Q}{\partial z}}\right)\,dy\,dz+\left({\frac {\partial P}{\partial z}}-{\frac {\partial R}{\partial x}}\right)\,dz\,dx+\left({\frac {\partial Q}{\partial x}}-{\frac {\partial P}{\partial y}}\right)\,dx\,dy{\Bigg )}\\[8px]&=\oint _{\partial \Sigma }{\Big (}P\,dx+Q\,dy+R\,dz{\Big )}\,,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89dbd321d685d332affbea97cda0374bc71d1333)
![{\displaystyle {\begin{aligned}&\int _{\Sigma }{\Big (}g\left(\nabla \times \mathbf {F} \right)+\left(\nabla g\right)\times \mathbf {F} {\Big )}\cdot d{\boldsymbol {\Sigma }}=\oint _{\partial \Sigma }g\mathbf {F} \cdot d\mathbf {r} \,,\\[8px]&\int _{\Sigma }{\Big (}\mathbf {F} \left(\nabla \cdot \mathbf {G} \right)-\mathbf {G} \left(\nabla \cdot \mathbf {F} \right)+\left(\mathbf {G} \cdot \nabla \right)\mathbf {F} -\left(\mathbf {F} \cdot \nabla \right)\mathbf {G} {\Big )}\cdot d{\boldsymbol {\Sigma }}=\oint _{\partial \Sigma }\left(\mathbf {F} \times \mathbf {G} \right)\cdot d\mathbf {r} \,,\\[8px]&\int _{\Sigma }(\nabla \mathbf {F} )\cdot d{\boldsymbol {\Sigma }}-(\nabla \cdot \mathbf {F} )d{\boldsymbol {\Sigma }}=\oint _{\partial \Sigma }d\mathbf {r} \times \mathbf {F} \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ddd158834c7a33aafbb1fd43396339e887bf9e0)









