منحنى بيانو

التكرارات الأربع الأولى في خط منحنى بيانو

منحنى بيانو (بالإنجليزية: Peano curve)‏ هو أول منحنيات ملء الفضاء المعرفة في تاريخ التحليل الرياضي تم تعريفها من طرف الرياضي الإيطالي جوزيبه بيانو في 1890.

هو منحنى مستو معرف بدالة متصلة وشمولية منطلقها مجال الوحدة $[0,1]$ ومستقرها $[0,1]^{2}$. الدالة شمولية بمعنى أنها تمر بكل نقط المربع، وهي بذلك تخط منحنى يملأ الفضاء الداخلي للمربع $[0,1]^{2}$.

هذا النوع من المنحنيات يدخل ضمن الكسيريات (Fractals) وبعد هاوسدورف الموافق لها يساوي 2. كان الرياضياتي الألماني جورج كانتور أول من لاحظ بأن $[0,1]$ و$[0,1]^{2}$ يمكن ربطهما بتطبيق تقابلي. هذا الأخير لا يمكن أن يكون متصلا، حسب برهنة يوجين نيتو. في حالة منحنى بيانو، فالتطبيق الموافق متصل وشمولي إلا أنه غير تبايني.

تعريف

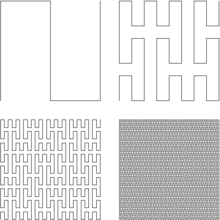
يتم بناء منحنى بيانو عبر الخوارزمية التالية :

1. في المرحلة الأولى، يتم تقسيم المربع $[0,1]^{2}$ إلى تسع مربعات متساوية المساحة. تكون المربعات مرقمة بطريقة يكون فيها لمربعين متتابعين ضلع مشترك، بدءا بالمربع الصغير السفلي الأيسر وانتهاء بالمربع العلوي الأيسر. يربط المحنى بين مراكز المربعات باتباع ترتيبها.
2. في المرحلة الثانية، يتم تقسيم كل مربع صغير من المربعات التسع (المستوى الأول) إلى تسع مربعات صغرى (المستوى الثاني). يتم ترقيمها بطريقة يكون فيها كل مربعين متتابعين من المستوى الثاني لهما ضلع مشترك، ويكون آخر مربع صغير من المستوى الثاني (داخل مربع من المستوى الأول) له ضلع مشترك مع أول مربع صغير في المربع من المستوى الأول الموالي. يربط المنحنى بين مراكز المربعات باتباع ترتيبها.
3. يتم تكرار العملية إلى ما لانهاية عبر مستويات تقسيم إضافية يربط فيها المنحنى بين مراكز المربعات المقسمة.

• خوارزمية خط منحنى بيانو
• 
  المرحلة 1 - بدء بتسع مربعات
• 
  المرحلة 2 - تقسيم إلى مربعات من المستوى 2
• 
  المرحلة 3 - تقسيم إلى مربعات المستوى 3
• 
  متاهة بيانو - المستوى 3

عند درجة التكرار $n$ تشكل المربعات متتالية $C_{n,0},C_{n,1},...,C_{n-1,9^{n-1}-1}$ ضلعها يساوي ${\frac {1}{3^{n}}}$.

يعرف منحنى بيانو التقريبي من الصنف الأول من الدرجة $n$ بالخط المتكسر (أو المنحنى المضلعي Polygonal curve) الذي يصل بين المراكز المتتابعة للمربعات المنشأة.

تعرف متاهة بيانو من الصنف الأول من الدرجة $n$ باتحاد جميع أضلاع المربعات المنشأة باستثناء الأضلاع المشتركة بين مربعين متتابعين (التي يقطعها منحنى بيانو من الدرجة $n$).

البناء التحليلي

في مقالته لسنة 1890، اقترح بيانو بناء تحليلي للمنحنى يقضي بإيجاد بدالة متصلة وشمولية $(x,y)$ منطلقها مجال الوحدة $[0,1]$ ومستقرها $[0,1]^{2}$ تربط كل $t\in [0,1[$ بنقطة $M(t)=(x(t),y(t))$.

اعتمد بيانو على خاصية إمكانية تطوير أي عدد حقيقي وفق نظام العد الثلاثي. كل $t\in [0,1[$ يمكن كتابته : $t=(0,a_{1},a_{2},...,a_{n},...)$ بحيث $(a_{n})_{n\in \mathbb {N} }$ هي متتالية الكتابة وفق العد الثلاثي ل $t$.

التطبيق المعرف للمنحنى يحقق ملء الفضاء الداخلي لمربع الوحدة : ${\begin{cases}x(t)=(0,b_{1},b_{2},...,b_{n},...)\\x(t)=(0,c_{1},c_{2},...,c_{n},...)\end{cases}}$ بحيث

• $b_{n}=a_{2n-1}$ إذا كان $a_{2}+a_{4}+...+a_{2n-2}$ زوجيا و $b_{n}=2-a_{2n-1}$ إذا كان $a_{2}+a_{4}+...+a_{2n-2}$ فرديا.
• $c_{n}=a_{2n}$ إذا كان $a_{1}+a_{3}+...+a_{2n-1}$ زوجيا و $c_{n}=2-a_{2n}$ إذا كان $a_{2}+a_{4}+...+a_{2n-2}$ فرديا.

وهكذا، بالنسبة لكل $t$، إذا كانت $K_{n}(t)$ متتالية مربعات متتابعة تؤول مساحة كل واحد منها إلى 0، فتقاطع المربعات يؤول إلى نقطة $M(t)=(x(t),y(t))$ تنتمي إلى منحنى بيانو. المنحنى المعرف مستمر وكثيف داخل مربع الوحدة $[0,1]^{2}$.

امتدادات

تم اقتراح منحنيات أخرى بعد ذلك من أهمها منحنى هيلبرت (1891) ومنحنى لوبيغ (1904) ومنحنى سيربينسكي (1912)، وكان آخر الاقتراحات المهمة تلك التي طورها الرياضياتي النمساوي والتر ووندرليتش سنة 1973.

• أمثلة لمنحنيات ملء فضاء أخرى
• 
  منحنى هيلبرت
• 
  منحنى ووندرليتش
• 
  منحنى سيربينسكي
• 
  منحنى لوبيغ