مستخدم:Ss walid/ملعب

المشتقة الثانية بالنسبة للدالة التربيعية ثابثة

المشتقة الثانية (بالإنجليزية: Second derivative)‏ هي مشتقة مشتقة الدالة عندما تكون معرفة. تُمكن من قياس تطور معدلات التغيرات. على سبيل المثال، المشتقة الثانية للإزاحة بالنسبة للأزمنة هي التغير في السرعة (معدل تغير الإزاحة)، أو التسارع.

دالة تتكون من متغير حقيقي واحد

إذا كانت الدالة تقبل مشتقة ثانية، نقول إنها من الصنف ^D2؛ إضافة إذا كانت هذه المشتقة الثانية متصلة، فإن الدالة من الصنف C ².

تدوين

إذا دوننا $f$ كدالة، إذن:

• تُدون المشتقة ب $f'$ أو ${\mathrm {d} f \over \mathrm {d} x}$
• تُدون المشتقة الثانية ب $f''=(f')'$ ($f$ الثانية) أو ${\mathrm {d} ^{2}f \over {\mathrm {d} x}^{2}}={\mathrm {d} \over \mathrm {d} x}\left({\mathrm {d} f \over \mathrm {d} x}\right)$.

التمثيل المبياني

تشير المشتقة الثانية إلى التغير في ميل المنحنى التمثيلي ويُمكن من قياس تقعر المنحنى. فإذا كانت موجبة في مجال ما، يزداد الميل، ويتجه الانحناء إلى الأعلى، وتسمى هذه الدالة ب " دالة محدبة " خلال هذا المجال. إذا كانت سالبة على مجال ما، يقل الميل، ويتجه الانحناء إلى الأسفل، وتسمى هذه الدالة ب " دالة مقعرة " خلال هذا المجال. وإذا كانت منعدمة، يكون المنحنى مستقيمًا محليًا. إذا المشتقة الثانية انعدمت وتغيرت الإشارة، لدينا نقطة انقلاب، وينعكس انحناء المنحنى.

تتيح هذه القيم أيضًا تقديم تفاصيل حول الحدود القصوى المحلية التي تتميز بانعدام المشتقة عند نقطة ما $x$:

• إذا $f'(x)=0$ و $f''(x)<0$، $f$ لديها حد أقصى محلي عند $x$:
• إذا $f'(x)=0$ و $f''(x)>0$، $f$ لديها قيمة دنيا محلية عند $x$:
• إذا $f'(x)=0$ و $f''(x)=0$، لا يمكننا أن نستنتج.

دالة لا تقبل مشتقة ثانية

الدوال الغير القابلة للاشتقاق عند نقطة ما لا تقبل مشتقة ثانية؛ وبالتحديد الدوال الغير المتصلة عند نقطة ما.

المشتقة العكسية للدالة المتصلة غير القابلة للإشتقاق هي دالة متصلة وقابلة للاشتقاق، ولكنها لا تقبل مشتقة ثانية عند النقاط التي تكون فيها الدالة الأولية غير قابلة للاشتقاق؛ هذه هي حالة المشتقة العكسية للمشتقة العكسية لدالة غير متصلة ولكن محدودة.

مثلاً، الدالة تشير:

$\operatorname {sgn}(x)=\left\{{\begin{matrix}-1&:x<0\\0&:x=0\\1&:x>0\end{matrix}}\right.$

بالنسبة للمشتقة العكسية الثانية:

$\iint \operatorname {sgn} :x\mapsto (x\times |x|)/2$

هذا المشتقة العكسية الثانية لا تقبل مشتقة ثانية عند 0.

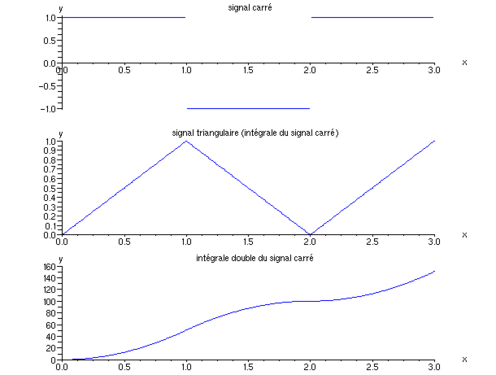
ومن الأمثلة الأخرى المشتقة العكسية للموجة المثلثية (مسننة)، والمشتقة العكسية المزدوجة للموجة المربعة، والمشتقة العكسية المزدوجة لدالة الجزء الصحيح.

• 
  المشتقة العكسية لدالة مسننة يمكن اشتقاقها مرة واحدة وليس مرتين.
• 
  المشتقة العكسية الثانية لدالة الجزء العشري قابلة للاشتقاق مرة واحدة وليس مرتين.
• 
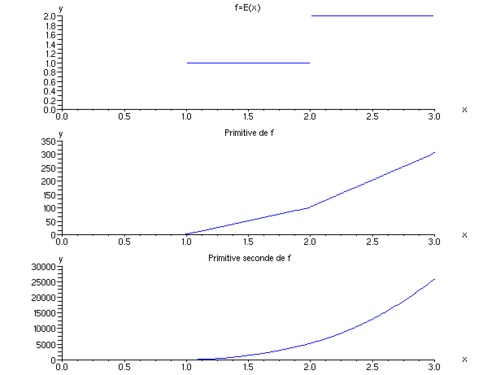
  المشتقة العكسية الثانية لدالة الجزء الصحيح قابلة للاشتقاق مرة واحدة وليس مرتين.

تعميم

بالنسبة للدالة ذو متغيرات $n$، يجب الأخد في الاعتبار الحالات الممكنة اعتمادا على المتغيرات. ثم يُعبر عن النتيجة في شكل مصفوفة هيسية.

انظر أيضًا

• تفاضل
• معادلة تفاضلية